Uma polia indicada na figura abaixo possui raio e momento de inércia de . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocidade do bloco de no momento em que ele atinge o solo.
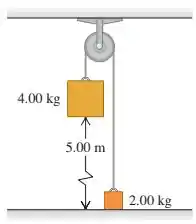
Passo 1
Falaaa, galeraaa! Como vocês estão? Vamos calcular a velocidade do bloco mais pesado quando ele atinge o solo. Para isso vamos usar as definições de conservação de energia e você verá nos passos como iniciar e chegar no resultado dessa questão.

Passo 2
Na posição inicial a energia potencial é zero. A energia cinética do sistema é a soma das energias cinéticas de cada objeto. Abaixo temos a figura que representa as forças advindas das massas.
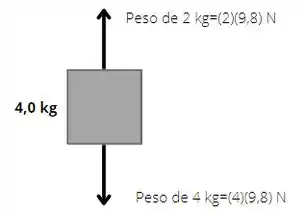
Na polia temos que
No bloco de podemos aplicar a segunda Lei de Newton:
Antes movimento, a energia gravitacional é
Passo 3
Com o movimento a energia potencial gravitacional é transformada em energia cinética. No fim do movimento, ou seja, quando o bloco toca o solo a energia potencial gravitacional será totalmente transformada em energia cinética. Dessa forma, a energia cinética será:
A energia cinética dos blocos é
Onde é a energia cinética relacionada ao movimento dos blocos e é a energia relacionada a rotação da polia.
Substituindo, temos
Podemos reescrever como
Podemos reorganizar
Colocando em evidência e substituindo valores:
Isolando :
Substituindo o valor de :
Então temos
Prontinho!
