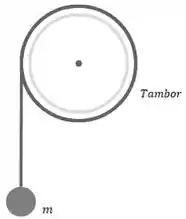
Engenheiros projetam um sistema por meio do qual uma massa em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (figura abaixo). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é . Nos testes na Terra, quando m possui e deve cair por , ela fornece de energia cinética ao tambor.
a) Quando o sistema for operado em Marte, qual a distância a massa de terá que cair para gerar o mesmo valor de energia cinética para o tambor?
Passo 1
E aí, pessoaaaal! Vamos resolver mais uma questão? Vamos descobrir aqui qual a distância necessária para que a massa possa gerar a mesma energia cinética quando o sistema funciona em Marte. Vamos fazer alguns passos para entender isso, tranquilo?

Passo 2
Observe que o corpo está em queda livre e preso a um tambor por um fio, que causa movimento no tambor, ou seja, temos transferência de energia.
Vamos aplicar a conservação de energia no sistema.
Temos que a energia cinética do tambor é
A energia cinética da massa será
E temos também que
Passo 3
Bom, se é o mesmo. Temos que é o mesmo e é o mesmo em ambos planetas. Dessa forma, é a mesma.
Ao tomar na altura inicial da massa e adotar para cima. Vamos dividir duas configurações:
1- Quando a massa está na posição inicial;
2- Quando a massa desce .
Então na configuração 1, temos:
E na configuração 2, temos:
Onde é a altura em que a massa desce.
Passo 4
Pela conservação de energia, temos que
Quando há elevação, que seria a situação 2, temos:
Porém, como e são iguais nos dois planetas, temos somente , então.
Isso nos leva a
Substituindo valores
Logo, a distância será
Prontinho, pessoal!
