Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Circular Acelerado

Ver Teoria
Exercício 121234567891011131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657

Enunciado

UnB, Física I, Lista 11, questão 5b

Um volante de raio igual a 0,300   m parte do repouso e se acelera com aceleração angular constante

de 0 ,   600   r a d / s 2 . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante

b) depois de ele ter girado um ângulo de 60,0 ° ;

Passo 1

Oi, pessoaaal! Como estão? Para resolver essa questãozinha, vamos calcular considerando que o volante já girou um pouco. Ao longo da resolução, veremos onde essa informação se encaixa, belê?

Passo 2

A aceleração tangencial é a aceleração que tangencia a curva do volante, passando na borda, como podemos ver na imagem. Já a aceleração radial é aquela que aponta para o centro da curva. A aceleração resultante, que é aquela proveniente da soma vetorial da aceleração tangencial e da aceleração radial.

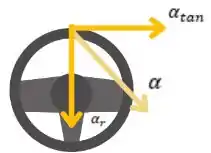
Passo 3

Vamos então calcular a aceleração tangencial utilizando a seguinte fórmula

α t a n = α ∙ r

Substituindo valores, temos

α t a n = 0,300   m ∙ 0,600   r a d / s 2

α t a n = 0,18   r a d / s 2

Passo 4

Para calcular a aceleração radial vamos precisar calcular a velocidade angular e saber qual a distância correspondente ao ângulo de 60,0   ° .

Então, a distância percorrida é dada por

θ = θ 0 = 60 π   r a d 180 = 1,047   r a d

Agora podemos calcular a velocidade angular

ω 2 = ω 0 2 + 2 α ∆ θ

Utilizando a raiz quadrada em ambos os lados da equação, temos

ω 2 = ω 0 2 + 2 α ∆ θ

ω = ω 0 + 2 α ∆ θ = 2 ( 0,600 ) ( 1,047 ) = 1,121   r a d / s

Calculando a aceleração radial, temos

α r = ω 2 ∙ r = 1,121 r a d s 2 ∙ 0,300   m

α r = 0,377 m / s 2

Passo 5

Assim, a aceleração resultante será dada por

α = α t a n 2 + α r 2

Substituindo valores

α = 0,377 2 + 0,18 2

α = 0,418   m / s 2

Até a próxima!

Resposta

α t a n = 0,18   r a d / s 2

α r = 0,377 m / s 2

α = 0,418   m / s 2

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c