Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Energia Cinética de Rotação

Ver Teoria
Exercício 161234567891011121314151718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899

Enunciado

UnB, Física I, Lista 11, questão 7

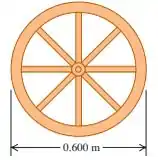
Uma roda de carroça é feita como indicado na figura abaixo. O raio da roda é igual a 0,300   m e possui massa igual a 1,40   k g . Cada um dos seus oito aros, distribuídos ao longo de diâmetros, possuem comprimento de 0,300   m e massa igual a 0,280   k g . Qual é o momento de inércia da roda em relação a um eixo perpendicular ao plano da roda e passando pelo seu centro?

Passo 1

Falaaaa aí, pessoal! Como vocês estão?

Nessa questão, precisamos considerar o momento de inércia provocado pelos 8 aros e pela roda. Vamos calcular o valor de ambos e somá-los para obter o valor total, beleza?

Passo 2

Podemos considerar cada aro como uma haste delgada com o eixo das abcissas passando por uma das extremidades. Dessa forma, o momento de inércia das 8 barras será dado por

I = 8 m L 2 3

Substituindo valores

I = 8 3 0,280   k g 0,300   m

Obtemos

I = 0,0672   k g m 2

Passo 3

O momento de inércia provocado pela massa da roda pode ser calculado por

I = m r 2

Substituindo valores, temos

I = 1,4   k g 0,30   m 2

Logo

I = 0,126   k g m 2

Passo 4

Agora podemos calcular o momento de inércia total, que será dado pela soma da inércia da roda e dos aros.

I = I r o d a + I a r o

Substituindo os valores já obtidos

I = 0,126   k g m 2 + - 0,0672   k g m 2

Assim, a inércia total é

I = 0,193   k g m 2

Prontinho, pessoal!

Resposta

I = 0,193   k g m 2

Exercícios de Livros Relacionados

Uma régua de um metro é mantida verticalmente com uma das extremidades apoiada no solo e depois liberada. Determine a velocidade da outra extremidade pouco antes de tocar o solo, supondo que a extremi
Na figura abaixo, uma barra fina e homogênea (com 4 m de comprimento e uma massa de 3 k g ) gira livremente em torno de um eixo horizontal A que é perpendicular à barra e passa por um ponto situado a
O corpo rígido da figura abaixo é formado por três bolas e três barras de ligação, com M = 1,6 k g , L = 0,6 m e θ = 30 ° . As bolas podem ser tratadas como partículas e as barras têm massa desprezíve
Como estagiário de uma empresa de engenharia, você é solicitado a medir o momento de inércia de uma grande roda, para girar em torno de um eixo que passa pelo seu centro. Você mede o diâmetro da roda,
91 . Na F I G U R AP D 12.91 , uma bola de gude desce rolando um trilho que possui uma parte em loop com raio R . A bolinha possui massa m e raio r . Que altura mínima h deve ter o trilho a fim de que