Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Circular Acelerado

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657

Enunciado

UnB, Física I, Lista 11, questão 5a

Um volante de raio igual a 0,300   m parte do repouso e se acelera com aceleração angular constante

de 0 ,   600   r a d / s 2   . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante

a) no início;

Passo 1

Falaa aí, pessoal! Tudo belezinha? O que precisamos calcular nessa questão são os três tipos de aceleração, tangencial, radial e resultante no início, ou seja, quando o volante ainda não deslocou percorrendo um raio.

Passo 2

Primeiro, vamos calcular a aceleração tangencial, beleza? Essa aceleração é aquela tangencia a curva do volante, ou seja, passa bem na borda. Veja só:

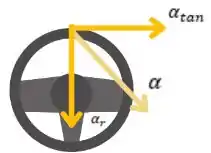
Para calcular, basta fazermos

α t a n = α ∙ r

α t a n = 0,300   m ∙ 0,600   r a d / s 2

α t a n = 0,18   r a d / s 2

Passo 3

Já a aceleração radial é aquela que aponta para o centro da curvatura. Aqui, como estamos calculando no início do movimento, temos que a velocidade angular é nula. Então

α r = ω 2 ∙ r = 0 2 ∙ 0,300 = 0

α r = 0

Passo 4

Agora podemos calcular a aceleração resultante, que é aquela proveniente da soma vetorial da aceleração tangencial e da aceleração radial.

α = α t a n 2 + α r 2

α = 0,18 2 + 0 2

Logo

α = 0,18   r a d / s ^ 2

Prontinho, galera!

Resposta

α t a n = 0,18   r a d / s 2

α r = 0

α = 0,18   r a d / s ^ 2

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c