UnB, Física I, Lista 11, questão 6b
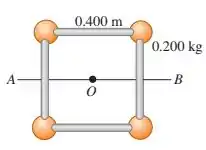
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:
c) passando pelo centro da esfera superior da esquerda e pelo centro da esfera inferior da direita e através do ponto 0.
Passo 1
E aí, tudo tranquilo para partir pra mais uma questão? Bom, precisamos calcular o momento de inércia de um corpo que possui uma massa e está localizado a uma certa distância do eixo de rotação. Nesse caso o eixo passará por duas bolinhas, então precisaremos calcular a inércia somente das bolinhas nos quais o eixo não passa por elas, belê? Vamos lá, sem dor de cabeça, entender isso.
Passo 2
Veja só por onde o eixo passa. Ele passará pela bolinha superior esquerda, pelo centro e pela bolinha inferior direita. Então somente as duas outras massas contribuirão.
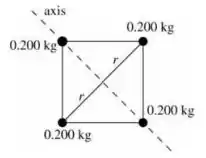
A distância será a equivalente a diagonal divido por dois, correto? Sendo , o lado do quadrado. Então podemos escrever:
Substituindo e calculando
Passo 3
De posse do valor da distância, podemos calcular o momento de inércia. Como temos quatro pontos, o momento de inércia total é, já que todas as massas contribuem
Podemos reescrever a expressão como
Por fim, basta substituir os valores
Prontinho! Partiu comprar um cafezinho?
