Listas de Estudos pra Prova - Halliday Vol 1 - 8°ed de Física 1 da UTFPR - Rotação

(Cap 10.2 – Ex. 1) Um bom lançador de beisebol pode arremessar uma bola a com uma rotação de . Quantas revoluções a bola realiza até chegar à base principal? Para simplificar, suponha que a trajetória de pés é percorrida em linha reta.

(Cap 10 – Ex 11) Um tambor gira em torno do eixo central com uma velocidade angular de . Se o tambor é freado a uma taxa constante de ,

(a) quanto tempo leva para parar?

(b) Qual é o ângulo total descrito pelo tambor até parar?

(Cap 10 – Ex 9) Um disco, inicialmente girando a , é freado com uma aceleração angular constante de módulo

(a) Quanto tempo o disco leva para parar?

(b) Qual é o ângulo total descrito pelo disco durante esse tempo?

(Cap 10.2 – Ex. 7) A roda da Fig. 10-27 tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos.

(a) Qual é a menor velocidade que a flecha deve ter?

(b) O ponto entre o eixo e a borda da roda por onde a flecha passa faz alguma diferença? Caso a resposta seja afirmativa, para que ponto você deve mirar?

(Cap 10 – Ex 12) Partindo do repouso, um disco gira em torno do eixo central com uma aceleração angular constante. O disco gira em . Durante esse tempo, qual é o módulo

(a) da aceleração angular e

(b) da velocidade angular média?

(c) Qual é a velocidade angular instantânea do disco ao final dos ?

(d) Com a aceleração angular mantida, que ângulo adicional o disco irá descrever nos seguintes?

(Capítulo 10.4 – Ex. 16) Um disco gira em torno do eixo central partindo do repouso com aceleração angular constante. Em um certo instante, está girando a ; após 60 revoluções, a velocidade angular é . Calcule (a) a aceleração angular, (b) o tempo necessário para completar 60 revoluções, (c) o tempo necessário para atingir a velocidade angular de e (d) o número de revoluções desde o repouso até o instante em que o disco atinge uma velocidade angular de .

(Cap 10 – Ex 17) Uma roda executa revoluções quando desacelera a partir de uma velocidade angular de até parar.

a) Supondo que a aceleração angular é constante, determine o tempo em que a roda leva para parar.

b) Qual é a aceleração angular da roda?

c) Quanto tempo é necessário para que a roda complete as primeiras revoluções?

(Cap 10.5 - Ex 27) Um método tradicional para medir a velocidade da luz utiliza uma roda dentada giratória. Um feixe de luz passa pelo espaço entre dois dentes situados na borda da roda, como na Fig. 10-31, viaja até um espelho distante e chega de volta à roda exatamente a tempo de passar pelo espaço seguinte entre dois dentes. Uma dessas rodas tem de raio e espaços entre dentes. Medidas realizadas quando o espelho está a uma distância da roda fornecem o valor de para a velocidade da luz.

a) Qual é a velocidade angular (constante) da roda?

b) Qual é a velocidade linear de um ponto da borda da roda?

(Cap 10.6 – Ex. 33) Calcule o momento de inércia de uma roda que possui uma energia cinética de quando gira a .

(Cap 10 – Ex 87) Uma roda de de raio está montada em um eixo horizontal sem atrito . O momento de inércia da roda em relação ao eixo é . Uma corda de massa desprezível está enrolada na roda e presa a um bloco de que escorrega em uma superfície horizontal sem atrito. Se uma força horizontal de módulo é aplicada ao bloco, como na Fig. 10-53, qual é o módulo da aceleração angular da roda? Suponha que a corda não desliza em relação à roda.

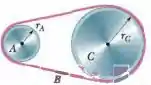
(Cap 10.7 – Ex. 35) Calcule o momento de inércia de uma régua de um metro, com uma massa de , em relação a um eixo perpendicular à régua na marca de. (Trate a régua como uma barra fina.)

(Cap 10.5 - Ex. 30) Na Fig. 10-32, uma roda de raio está acoplada por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda e atinja uma velocidade angular de , supondo que a correia não desliza. (Sugestão: se a correia não desliza, as velocidades lineares das bordas dos discos são iguais.)

(Cap 10 – Ex 69) Na Fig. 10-49, dois blocos de estão ligados por uma corda de massa desprezível que passa por uma polia de de raio e momento de inércia . A corda não escorrega na polia; não se sabe se existe atrito entre a mesa e o bloco que escorrega; não há atrito no eixo da polia. Quando o sistema é liberado a partir do repouso, a polia gira de em e a aceleração dos blocos é constante. Determine

a) o módulo da aceleração angular da polia,

b) o módulo da aceleração de cada bloco,

c) a tensão , da corda e

d) a tensão da corda.

(Cap 10 – Ex 39) Na Fig. 10-36, duas partículas, ambas de massa , estão ligadas uma à outra, e a um eixo de rotação em , por duas barras finas, ambas de comprimento e massa . O conjunto gira em orno do eixo de rotação com velocidade angular . Em relação a , quais são

a) o momento de inérica do conjunto e

b) a energia cinética do conjunto?

(Cap 10 – Ex 67) Uma chaminé cilíndrica cai quando a base sofre um abalo. Trate a chaminé como uma barra fina com de comprimento. No instante em que a chaminé faz um ângulo de com a vertical durante a queda, qual é

a) a aceleração radial do topo e

b) a aceleração tangencial do topo? (Sugestão: use considerações de energia e não de torque.)

c) Para que ângulo a aceleração tangencial é igual a ?

(Cap 10 – Ex 93) Na Fig. 10-56, uma roda com de raio é montada em um eixo horizontal sem atrito. Uma corda de massa desprezível é enrolada na roda e presa a uma caixa de que escorrega sobre uma superfície sem atrito com uma inclinação em relação à horizontal . A caixa escorrega para baixo com uma aceleração de . Qual é o momento de inércia da roda em relação ao eixo?

(Cap 10 – Ex 49) No inicio de um salto de trampolin, a velocidade angular de uma mergulhadora em relação a um eixo que passa pelo centro de massa varia de zero a em . Seu momento de inércia em relação ao mesmo eixo é de . Durante o salto, quais os módulos

a) da aceleração angular média da mergulhadora e

b) do torque externo médio exercido pelo trampolim sobre a mergulhadora?

(Cap 10 – Ex 57) Uma polia, com um momento de inércia de em relação ao eixo e um raio de , é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo com a equação , com em newtons e em segundos. A polia está inicialmente em repouso. Em , quais são

a) a sua aceleração angular e

b) sua velocidade angular?