Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 2112345678910111213141516171819202223242526272829

Enunciado

Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção 7, Exercício 35

(Cap 10.7 – Ex. 35) Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56   k g , em relação a um eixo perpendicular à régua na marca de   20   c m . (Trate a régua como uma barra fina.)

Passo 1

Faaala, galerinha! Tudo certinho? Bora lá resolver mais uma questãozinha?

Essa questão aqui pede pra gente o momento de inércia de uma régua perpendicular a um eixo, em uma marca de 20 cm. O enunciado aqui dá uma dica bem bacana, dizendo que podemos adotar a régua como sendo uma barra fina! Tá, mas porque isso ajuda a gente?

Já que adotaremos a régua como uma barra fina, vamos ter uma configuração mais ou menos igual a isso aqui:

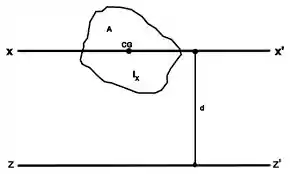
Onde d representaria a régua, e x o eixo perpendicular a ela igual comentamos.

Essa figura aqui em cima representa um modelo clássico do teorema dos eixos paralelos, que permite calcular o momento de inércia de um sólido relativo a um eixo.

A fórmula referente a esse teorema se dá por: I   =   I C M   +   M h 2 , em que I C M é o momento de inércia em relação ao centro de massa, M é a massa e h é a distância entre o centro de massa e o eixo de rotação considerado.

Passo 2

Então, vamos começar encontrando o centro de massa h da nossa régua:

Como o centro de massa está no centro da régua, temos que:

h   =   0,50   m   –   0,20   m   =   0,30   m

Então, quando formos calcular o I C M , vamos ter que:

I C M = 1 12 M L 2 = 1 12 0,56   k g 1   m 2 = 4,67 * 10 - 2   k g . m 2

Agora que já temos tudo o que precisamos para substituir no teorema dos eixos paralelos, temos que:

I = 4,67 * 10 - 2 k g . m 2 + 0,56   k g 0,30   m 2

I = 9,7 * 10 - 2 k g . m 2

Isso é a Física! Doce como o mel...

Para essa questão é isso pessoal! Bora resolver mais uma?

Resposta

I = 9,7 * 10 - 2 k g . m 2

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.