Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção 5, Exercício 30
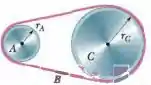
(Cap 10.5 - Ex. 30) Na Fig. 10-32, uma roda de raio está acoplada por uma correia a uma roda de raio . A velocidade angular da roda é aumentada a partir do repouso a uma taxa constante de . Determine o tempo necessário para que a roda e atinja uma velocidade angular de , supondo que a correia não desliza. (Sugestão: se a correia não desliza, as velocidades lineares das bordas dos discos são iguais.)
Passo 1
Faaaala, meu povo! Tudo certinho? Partiu resolver mais um exercício?
Então galera, esse exercício é daqueles típicos de rotação e o enunciado deu uma dica bem bacana pra gente, que vai ajudar bastante!
Ele disse que: como a correia não desliza, as velocidades lineares das bordas dos discos são iguais. Tá, mas como isso ajuda a gente aqui?
Isso significa que um ponto da borda da roda tem a mesma aceleração tangencial que um ponto da borda da roda . E isso vai ser a sacada pra gente resolver o exercício de maneira bem simples!
Passo 2
O nosso próximo passo aqui vai ser encontrar a acelaração angular da roda , pois a partir dela, será possível determinar o tempo pra roda atingir a velocidade angular dada no enunciado.
A nossa interpretação feita ali no passo 1 significa que , onde é a aceleração angular da roda e é a aceleração angular da roda .
Então, tendo em vista isso, conseguimos determinar a primeira informação que precisamos:
Por fim, como a velocidade angular da roda é dada por , o tempo para que a roda atinja uma velocidade angular a partir do repouso é:
Prontinho, pessoal! Bem simples, não é mesmo? Bora lá resolver mais uma então?
