Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção 2, Exercício 7
(Cap 10.2 – Ex. 7) A roda da Fig. 10-27 tem oito raios de igualmente espaçados, está montada em um eixo fixo e gira a . Você deseja atirar uma flecha de de comprimento paralelamente ao eixo da roda sem atingir um dos raios. Suponha que a flecha e os raios são muito finos.
(a) Qual é a menor velocidade que a flecha deve ter?
(b) O ponto entre o eixo e a borda da roda por onde a flecha passa faz alguma diferença? Caso a resposta seja afirmativa, para que ponto você deve mirar?
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
Vamos começar interpretando o conceito do exercício. Para não se chocar com os raios, a flecha deve passar pela roda em um tempo menor que
Ou seja, como a roda tem raios, a cada de volta teremos um possível ponto de contato com a flecha. E como a roda gira vezes por segundo, a cada segundo um raio fica na posição que queremos evitar. Concluindo, a velocidade tem que ser suficiente para que atravesse todos os seus de comprimento num intervalo igual ou menor que .
A velocidade mínima da flecha é, portanto:
Passo 2
Vamos pensar agora no item (b).
Em nenhum momento consideramos a posição radial por onde a flecha passará. Posição radial, o que é isso?
Imagine o centro da roda. Se ligassemos o ponto onde a flecha atravessa a roda ao ponto de centro da roda encontraríamos um raio qualquer. Veja:
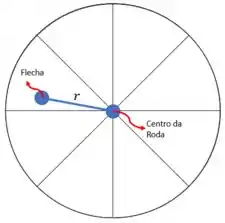
Se essa posição fosse importante para o nosso modelo, em algum momento teríamos inserido o valor de nos cálculos.
Portanto a resposta é Não.
Isso é a Física! Doce como o mel...
Para essa questão é isso pessoal! Bora resolver mais uma?
Resposta
(a)
(b) Não.