Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção Problemas Adicionais, Exercício 87
(Cap 10 – Ex 87) Uma roda de de raio está montada em um eixo horizontal sem atrito . O momento de inércia da roda em relação ao eixo é . Uma corda de massa desprezível está enrolada na roda e presa a um bloco de que escorrega em uma superfície horizontal sem atrito. Se uma força horizontal de módulo é aplicada ao bloco, como na Fig. 10-53, qual é o módulo da aceleração angular da roda? Suponha que a corda não desliza em relação à roda.
Passo 1
Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?
A força aplicada faz o bloco acelerar e, com isso, a roda é submetida a um torque que produz uma aceleração angular.
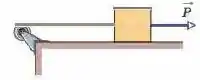
Vamos tomar o sentido para a direita como positivo e uma rotação no sentido anti-horário como positiva (que é o sentido convencional). Nesse caso, vamos chamar a aceleração do bloco de . Aplicando ao bloco a Segunda Lei de Newton, obtemos:
Em que é a tensão da corda. Aplicando à roda a Segunda Lei de Newton (para rotações), obtemos
E como a aceleração angular se relaciona com a aceleração linear através da relação:
Teremos que:
Tal que:
Passo 2
Legal, agora substituindo essa informação na equação , obtemos:
Assim, a aceleração angular será:
Então para , , e , temos:
o que nos dá
Isso é a Física! Doce como o mel...
Para essa questão é isso pessoal! Bora resolver mais uma?
