Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 3912345678910111213141516171819202122232425262728293031323334353637384041424344454647

Enunciado

Livro Halliday, Volume 1, 8ª edição, Capítulo 10, Seção Problemas Adicionais, Exercício 69

(Cap 10 – Ex 69) Na Fig. 10-49, dois blocos de 6,20   k g estão ligados por uma corda de massa desprezível que passa por uma polia de 2,40   c m de raio e momento de inércia 7,40 * 10 - 4 k g · m 2 . A corda não escorrega na polia; não se sabe se existe atrito entre a mesa e o bloco que escorrega; não há atrito no eixo da polia. Quando o sistema é liberado a partir do repouso, a polia gira de 0,650   r a d em 91,0   m s e a aceleração dos blocos é constante. Determine

a) o módulo da aceleração angular da polia,

b) o módulo da aceleração de cada bloco,

c) a tensão T , da corda e

d) a tensão   T 2 da corda.

Passo 1

Faala, meu povo! Tudo bem com vocês? Partiu resolver mais um exercício?

Começaremos o exercício escolhendo sistemas de coordenadas diferentes para os dois blocos para que a aceleração de ambos seja positiva, o que nos permite escrever a 2   =   a 1   =   R α = a .

Assim, escolhemos o sentido para a direita como positivo para o bloco 2, o sentido para baixo como positivo para o bloco 1 e, ao contrário da convenção usual, o sentido horário de rotação da polia como positivo. Isso significa que interpretamos o valor de θ dado no problema como um valor positivo.

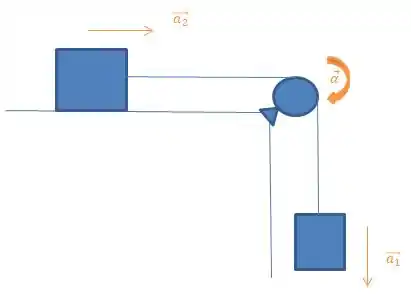
Aplicando a Segunda Lei de Newton às duas massas e à polia, obtemos as três equações a seguir:

Bloco 1:

↓ ∑ F y = m a

m 1 g - T 1 = m 1 a 1

Bloco 2:

→ ∑ F x = m a  

T 2 - f 2 = m 2 a 2

Polia:

↻ ∑ τ = I α  

T 1 R - T 2 R = I α

Usando a equação horária da posição angular para um movimento circular acelerado, teremos:

θ = ω 0 t + 1 2 α t 2

Como a nossa polia parte do repouso ( ω 0 = 0 ) e conhecemos algumas variáveis dadas no enunciado, podemos encontrar a nossa aceleração angular:

θ = 0 + 1 2 α t 2

α = 2 θ t 2 = 2 0,130 r a d 0,091   s 2 = 31 , 4   r a d / s 2

Passo 2

Continuando, temos o valor do α agora, a aceleração angular da nossa polia.

Podemos usar essa aceleração angular, para encontrar a aceleração tangencial na superfície da polia!

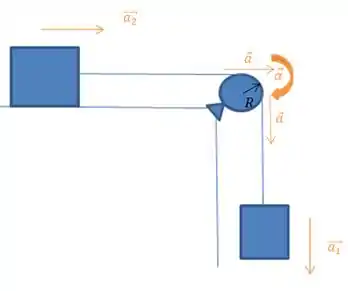
E essa aceleração é a mesma aceleração que os blocos irão possuir!

α = 2 R θ t 2

a = 2 0.024 m 0.130 r a d 0.0910   s 2

α = 0 , 754   m / s 2

Passo 3

Agora vamos olhar para primeira equação do Passo 1 e substituir as massas e a aceleração para conseguir o valor de T 1 :

T 1 = m 1 g - 2 R θ t 2 = 6,2 ( 9,8 - 2 0.024 m 0.130 r a d 0.0910   s 2 ) = 56 , 1   N

Passo 4

Faremos o mesmo para a terceira equação, obtemos o valor de T 2 :

T 2 = T 1 - I α R = 56.1 - 7,4 * 10 - 4 k g ⋅ m 2 31.4 r a d s 2 0,024 m = 55 , 1 N

Isso é a Física! Doce como o mel...

Para essa questão é isso pessoal! Bora resolver mais uma?

Resposta

a) α = 31 , 4   r a d / s 2

b) a = 0,754   m / s 2

c) T 1 = 56 , 1   N

d) T 2 = 55 , 1   N

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,