Uma associação de estudantes universitários de uma grande universidade deseja saber a opinião dos alunos sobre a proposta da reitoria a respeito do preço do bandejão. Para isso, selecionou-se aleatoriamente uma amostra de 200 estudantes, dos quais se verificou que 140 estudantes são favoráveis à proposta da reitoria.

a) Determine o intervalo de confiança para a verdadeira proporção de alunos favoráveis à política da reitoria, ao nível de significância de 2%.

b) Qual deverá ser o tamanho da amostra para a verdadeira proporção de alunos favoráveis à política da reitoria com um erro máximo de 3%, i.e. para que o raio do intervalo de confiança seja inferior a 3%, ao mesmo nível de significância do item (a).

Como estimador para , vamos usar

Logo,

Queremos achar um intervalo em torno da média que corresponde a uma probabilidade de pois o nível de significância é de . Para achar esse intervalo em torno da média, fazemos a tradicional mudança de variável:

Queremos que

Como tem média , podemos escrever

Logo,

Agora que achamos a probabilidade de ser menor que , podemos ir para a tabela:

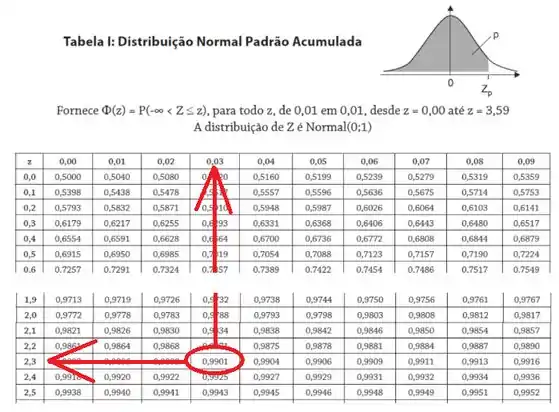
Tiramos que

Os valores de que corresponde aos valores limites de são:

Substituindo os números:

Portanto, o intervalo de confiança para a proporção é

No item (b) queremos saber qual deve ser o tamanho da amostra para que o tamanho do intervalo de confiança seja , isso significa que

Logo,

Como o nível de significância é o mesmo, o valor de é o mesmo do item (a):

Logo,

Usando a fórmula de :

Elevando ao quadrado os dois lados da equação:

Portanto, precisaríamos de um pouco mais de 5 mil pessoas. Para termos intervalos de confiança mais estreitos, precisamos de amostras bem maiores!