Um dos centros acadêmicos da POLI está elaborando uma pesquisa para saber a opinião dos alunos de graduação da escola sobre certa medida proposta pela Reitoria da USP. Os alunos devem basicamente responder se são favoráveis ou não à medida. Considerando um nível de confiança de e uma margem de erro de , qual deve ser o número máximo de alunos entrevistados pelo centro acadêmico?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Essa questão é bem direta, mas antes vamos analisar o que a questão pede.
Foram dados alguns parâmetros como o nível de confiança e a margem de erro o que a pesquisa pretende obter. Não temos informações da proporção das amostras que queremos obter, portanto vamos usar a equação que determina o número máximo de amostras com base no nível de confiança e na margem de erro, onde
Vamos organizar os dados que temos:
Passo 2
se trata do valor decimal da margem de erro .
se trata de um índice relacionado ao nível de confiança que vemos na tabela abaixo
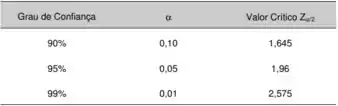
Substituindo esses valores na equação , temos que:
Calcula música número máximo de amostras é de , como não é possível um número de amostras ser fracionário, devemos considerar o número inteiro maior do que o valor calculado.
Portanto o número máximo de alunos que devem ser entrevistados é de alunos!, ou seja a famosa letras C de Cristo.

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
C)