Considere o seguinte gráfico mostrando o fluxo do campo magnético através de uma espira isolante em repouso, como função do tempo. Assinale a opção que melhor representa a força eletromotriz ao longo da espira, como função do tempo, nos intervalos de tempos típicos do gráfico, respectivamente.
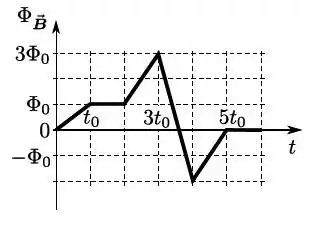
- , , , , ,
- , , , , ,
- A fem é sempre zero, pois, a espira é isolante.
- , , , , ,
- , , , , ,
Passo 1
Lei de Faraday na cara. Temos que a força eletromotriz é igual à:
Basta derivar e trocar o sinal, lembrando que para o caso de uma reta, a derivada é igual ao coeficiente angular desta. Logo, para cada intervalo de tempo:
Passo 2
Passo 3
Passo 4
Passo 5
Passo 6
Resposta
Letra a