Uma espira condutora quadrada de lado encontra-se sobre o plano de um sistema de coordenadas com dois de seus vértices sobre os pontos e deste plano. Ela está imersa em uma região de campo magnético dado por , onde e são constantes positivas. Qual é o módulo da força eletromotriz induzida sobre a espira em um instante ?
Passo 1
Cara... O módulo da força eletromotriz de acordo com a Lei de Faraday pode ser calculado por...
Onde é o fluxo de campo elétrico dentro da região da espira.
No nosso caso, estamos falando de uma espira quadrada de lado posicionada no plano desse modo aqui...
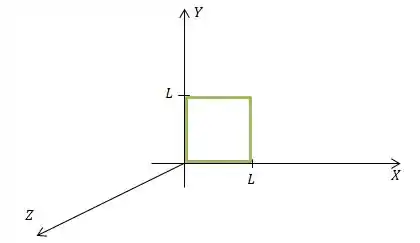
Então partiu calcular o fluxo do campo elétrico dentro dessa espira primeiro?
Passo 2
Cara, de acordo com a teoria, podemos calcular o fluxo de um campo magnético por uma integral de superfície...
Onde representa a superfície da espira quadrada.
Pow... Olhando para o nosso quadrado novamente, vamos perceber que o vetor normal a sua superfície é está na direção do eixo ...
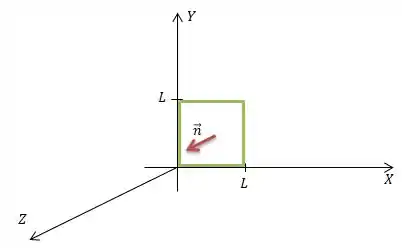
Então, podemos dizer que...
Ou ainda...
Logo, o produto escalar entre o campo magnético e o vetor normal ...
Logo, a integral de superfície se resume a uma...
ORA! A integral de , de acordo com a nossa teoria de calculo, representa a área da superfície (do quadrado de lado )...
Passo 3
Com o fluxo do campo magnético calculado, podemos então determinar a força eletromotriz pela derivada da Lei de Faraday...
Resposta
Letra A.