Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Trabalho, Energia e Força Eletromotriz

Ver Teoria
Exercício 101234567891112131415161718192021222324

Enunciado

Uma espira quadrada de lado 2 a , resistência R e massa m é lançada com velocidade inicial v 0 para a direita em direção a uma região de largura 2 b ( b > a ) onde há um campo magnético uniforme de módulo B perpendicular ao plano do papel e apontando para fora dele. Enquanto a espira entra na região com campo magnético (ou seja 0 < x x < 2 a ) determine:

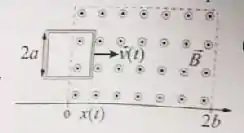
  1. O fluxo em função da posição do início da espira x t ;
  2. A f e m induzida na espira;
  3. O módulo e o sentido da corrente induzida na espira, justificando a resposta em termos da Lei de Lenz;
  4. Os vetores força magnética e aceleração na espira em função do tempo;
  5. A velocidade da espira em função do tempo;
  6. Qual deve ser a mínima velocidade inicial v 0 (em termos dos outros parâmetros do problema), para que o início da espira atinja a outra extremidade da região contendo o campo magnético?

Passo 1

L e t r a   A :

O fluxo magnético ϕ sempre pode ser dado por uma integral de superfície:

ϕ = ∬ B →   d A →

Mas olha que maravilha! O campo B que atravessa a região da espira é perpendicular a área da espira, veja:

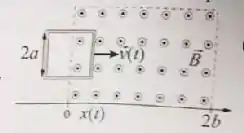
Ou seja, B → é perpendicular ao vetor área d A → . Na matemática, toda vez que temos o produto vetorial de dois vetores perpendiculares, o resultado será o produto do módulo dos dois vetores: B →   d A → = B   d A .

ϕ = ∬ B   d A       →

ϕ = B ∬ d A  

ORA! A integral de d A é a área da região da espira que tem campo atravessando. No caso é o retângulo de comprimento 2 a e largura x x ...

ϕ = B   2 a ⋅ x t     →

ϕ = 2 a B   x t

Passo 2

L e t r a   B :

Pela Lei de Faraday-Lenz a f e m   ε induzida na espira será...

ε = - d ϕ d t     →

ε = - d d t 2 a B   x t     →

ε = - 2 a B d d t x t     →

Só que o que vem a ser d x / d t ?

SIM! É a velocidade da espira! Então...

ε = - 2 a B v t

Passo 3

L e t r a   C

O módulo da corrente que aparece na espira pode ser dado simplesmente pela Lei de Ohm...

ε = I R   →

I = ε R = 2 a B v t R

O sentido da corrente tem que obedecer a Lei de Lenz: a corrente que surge deve possuir um campo magnético induzido de modo a se opor a direção do fluxo externo.

No nosso caso, temos um fluxo externo apontado para cima (saindo da sua telinha)...

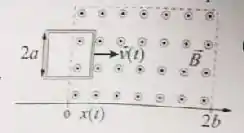
Então a corrente deve ser de modo que o fluxo produzido por ela seja para baixo (entrando na telinha) para se opor ao fluxo externo, ta ligado? Pela regra da mão direita, a corrente que gera tal fluxo deve estar no sentido horário.

Passo 4

L e t r a   D :

POW! A medida que a espira entra na região de campo magnético, surge uma força que empurra os elétrons da corrente para cima no lado 2 a da frente:

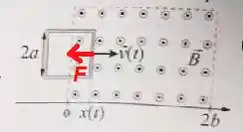
Podemos calcular essa força pela fórmula...

F = I 2 a B   →

F = 2 a B v t R 2 a B   →

F = 4 a 2 B 2 v t R

A direção da força é a direção do vetor velocidade, porém negativo...

F → = - 4 a 2 B 2 v → t R

A aceleração, vai ser a força dividido pela massa do elétron...

a → = F → m = - 4 a 2 B 2 v → t m R

Passo 5

L e t r a   E

POW! Sabemos que a aceleração pode ser dada por...

a = d v d t = - 4 a 2 B 2 v m R

Passando o v de um lado e o d t do outro...

d v v = - 4 a 2 B 2 m R   d t

Para simplificar, podemos chamar essa constante 4 a 2 B 2 / m R de α ...

d v v = - α   d t   →

Integrando de ambos os lados...

∫ d v v = ∫ - α   d t   →

ln ⁡ v = - α t + C   →

v = e - α t + C

Bem, como e a + b = e a e b ...

v = e C e - α t

Como C é uma constante, e C é uma constante e que dependerá da condição inicial sobre a velocidade, isto é, da velocidade inicial v 0 ...

v = v 0 e - α t

Passo 6

L e t r a   F

Bem, quando a espira fica completamente imersa no campo magnético, não terá mais variação de campo magnético, então não terá mais f e m induzida e, portanto, não terá mais corrente. Logo, a força magnética será nula!

A força sendo nula, a espira permanecerá com a velocidade v 1 de quando ela termina de entrar no campo. Primeiro devemos encontrar qual será essa velocidade, vamos nessa?

Passo 7

A velocidade v 1 em termos do tempo t 1 que a espira leva para entrar completamente na região é...

v 1 = v 0 e - α t 1   →

POW! Sabemos assim que a espira terminar de entrar na região, x t 1 = 2 a . Então, vamos encontrar x t primeiro...

v = d x d t   →

x t = ∫ v   d t   →

Substituindo e integrando...

x t = ∫ v 0 e - α t   d t   →

x t = v 0 e - α t - α + C

Sabemos que em t = 0 , x 0 = 0 ...

0 = v 0 e 0 - α + C   →

C = v 0 α

Logo, o deslocamento x t pode ser dado por...

x t = v 0 e - α t - α + v 0 α

Ou...

x t = v 0 α 1 - e - α t

Como x t 1 = 2 a ...

2 a = v 0 α 1 - e - α t 1     →

2 a = 1 α v 0 - v 0 e - α t 1     →

E olha que maneiro! Quem é v 0 e - α t 1 ?

2 a = 1 α v 0 - v 1     →

2 a α = v 0 - v 1     →

Ou seja, a velocidade inicial em termos da velocidade v 1 será...

v 0 = 2 a α + v 1

Como v 1 pode ser pequeno, mas ele tem que ser v 1 > 0 (se ele for igual a 0 a espira para de se movimentar), temos que ter...

v 0 > 2 a α

Se isso acontecer, então a gente garante que a espira atravessa a região .

Resposta

Letra A: ϕ = 2 a B   x t

Letra B:

ε = - 2 a B v t

Letra C:

I = 2 a B v t R       ( s e n t i d o   h o r á r i o )

Letra D:

F → = - 4 a 2 B 2 v → t R             e             a → = - 4 a 2 B 2 v → t m R

Letra E:

v = v 0 e - α t       o n d e         α = 4 a 2 B 2 m R

Letra F:

v 0 > 2 a α

Exercícios de Livros Relacionados

Uma lâmpada fluorescente compacta custa aproximadamente R $10,00 e tem um tempo de vida típico de 10.000h . A lâmpada usa 20W de potência, mas produz iluminação equivalente à de uma lâmpada incandesce
Uma bateria com fem de 6,0V e resistência interna de 0,30Ω é conectada a um resistor variável com resistência R . Determine a corrente e a potência fornecida pela bateria quando R é (a) 0 , (b) 5,0Ω ,
Uma aquecedor de 1,00k W é projetado para operar a 240V . (a) Qual é a resistência do aquecedor e qual é a corrente nos fios que fornecem potência para o aquecedor. (b) Qual é a potência fornecida ao
A corrente medida em um circuito na casa do seu tio é 12,5A . Neste circuito, o único equipamento que está ligado é um aquecedor de ambiente que está sendo utilizado para aquecer o banheiro. Um par de
Os grandes eletroímãs convencionais utilizam o arrefecimento de água para evitar o aquecimento excessivo das bobinas magnéticas. Um grande eletroímã de laboratório transporta uma corrente igual a 100A