Uma espira quadrada de lado , é girada com uma frequência constante num campo magnético uniforme , entrando no plano da página, como mostra a figura abaixo. Considere a resistência total do sistema igual a . Calcule:
A força eletromotriz induzida na espira.
A máxima induzida na espira.
A corrente induzida na espira. No momento em que a espira começa a girar, qual o sentido da corrente induzida (horário ou anti-horário), considere o início igual ao desenho abaixo.
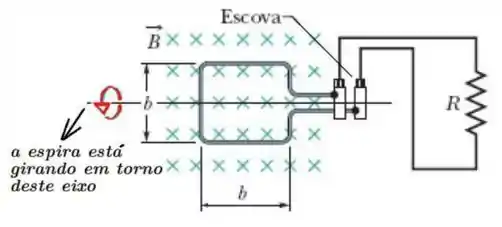
Passo 1
Fala aí pessoal, tudo bem?
Nessa questão temos um probleminha sobre força eletromotriz induzida. Basicamente, temos uma espira que está girando em uma região de campo magnético constante e que está conectada a um circuito de resistência . O enunciado nos faz algumas perguntas sobre a induzida, a máxima induzida, e a corrente induzida na espira.
Para responder essas perguntas é fundamental lembrarmos da Lei de Faraday.
E, também, devemos lembrar que o fluxo magnético é dado por:
Onde é o campo magnético atuando na espira, é a superfície delimitada pela espira, e é a área da mesma.
Como no nosso enunciado o campo magnético é constante, essa expressão se reduz a:
Mas, essa integral a área total da espira. Logo:
Então pessoal, o nosso fluxo vai estar variando com o tempo justamente porque o ângulo da área com o campo está variando. Isso irá gerar a induzida.
Daí, vamos escrever em função do tempo para usarmos a lei de Faraday e calcular a induzida.
Passo 2
No item , precisamos determinar a induzida.
Pra começar, vamos escrever a expressão do fluxo do campo magnético em função do tempo.
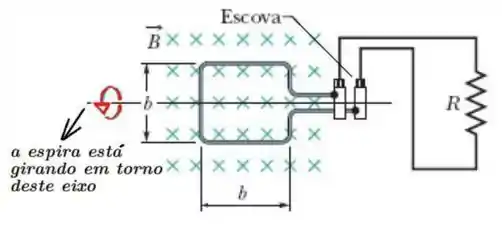
Como a espira está girando, com uma frequência , temos que:
Como essa velocidade angular é constante, temos:
Inicialmente, o ângulo entre o campo magnético e a espira é de . Assim:
Logo, como o fluxo magnético é dado por:
Substituindo o valor de , vem:
Assim, usando a lei de Faraday, temos:
Como e são constantes:
Logo:
Como a área da espira é dada por:
Finalizamos a induzida com:
Muito bom!
Passo 3
No item precisamos determinar a máxima induzida.
Ué, como assim máxima?
Então, é que como a gente viu no item anterior, a induzida varia com o tempo, segundo a expressão:
Assim, precisamos verificar o valor máximo dessa expressão.
Mas, como a dependência dela com o tempo está apenas no argumento do seno, e sabemos que a função seno varia entre e , podemos afirmar que a será máxima quando o seno for máximo. Logo, temos:
Aeee! Tudo tranquilo até aqui?
Passo 4
Pra finalizar, precisamos determinar o valor da corrente no circuito, bem como o seu sentido assim que a espira começa a girar. Então, pra determinar a corrente basta usarmos a lei de Ohm:
Como no nosso circuito temos apenas um resistor de resistência , temos:
Assim:
Substituindo o valor que encontramos para , temos:
Agora precisamos apenas determinar o sentido da corrente.
Pela Lei de Lenz, o sentido da corrente induzida produzir um fluxo magnético que se oponha a variação do fluxo que gerou a corrente.
ÉOQ? HAHA
Calma, se temos uma variação do fluxo aumentando, a corrente induzida por essa variação deve produzir um fluxo oposto a esse aumento. Se o fluxo estiver diminuindo, a corrente induzida por essa variação deve produzir um fluxo que se oponha a essa diminuição, sacou?
A ideia é que a corrente induzida vai gerar um fluxo que tente fazer tudo voltar a ser como era antes.
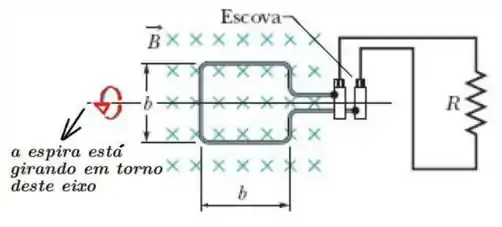
Assim, na nossa espira, quando ela começa a girar o fluxo que está passando na espira diminui. Dessa forma, a corrente gerada precisa compensar essa diminuição fazendo o fluxo aumentar. Ou seja, precisamos de uma corrente no circuito que provoque um aumento de fluxo no mesmo sentido que estava antes.
Em outras palavras, queremos que a corrente faça o fluxo aumentar entrando no plano da espira. Usando a regra da mão direita, basta que a corrente esteja no sentido horário. Assim, quando “agarrarmos” a espira, o polegar irá apontar para dentro dela (o que representa o sentido do campo magnético).
Sacaram a ideia?
Então é isso pessoal, muito obrigado pela atenção e até a próxima 😊