Um carrossel tem uma área de e gira a em torno de um eixo vertical num lugar onde o campo magnético da Terra é vertical e uniforme, de intensidade . A induzida no contorno do carrossel é:
- Zero;
Passo 1
POW! Mano, pode anotar aí o que eu vou te dizer: se um problema te der campo magnético e te pedir para você encontrar (força eletromotriz ), então provavelmente você utilizará a Lei de Faraday-Lenz:
Onde representa o fluxo do campo magnético, e a derivada representa justamente a variação desse fluxo no tempo dentro de uma área, neh.
Como a gente está buscando a no contorno de uma área, eu acho interessante primeiro a gente desenhar essa região, partiu?
Passo 2
No nosso caso, queremos encontrar à no contorno do carrossel representado por essa circunferência girando:

O campo magnético atravessa a área desse carrossel na direção vertical:
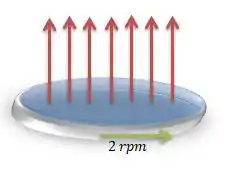
Bem, agora é hora de interpretar esse desenho de acordo com a nossa Lei de Faraday-Lenz do passo anterior. Bora?
Passo 3
POW! De acordo com a equação...
Só existe se existir variação de fluxo dentro da região. Só que tipo...
- O nosso campo é de intensidade constante .
- Além disso, ele atravessa uma região de área fixa () e que, embora ela esteja girando, a área que o campo magnético atravessa é exatamente a mesma ().
Se a área que o campo atravessa não muda, e nem o campo, então não tem variação de fluxo! Ou seja...
Portanto, a induzida tem valor...
Resposta
Letra A.