Um indutor , um resitor e uma fonte de são ligados em série a uma chave . Em a chave é fechada neste instante é zero. Depois de um tempo qual será a tensão no indutor?
Passo 1
Antes do , temos aqui o seguinte circuito...
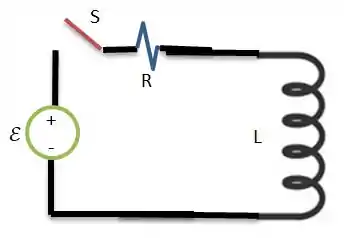
Assim que a chave fecha em ...
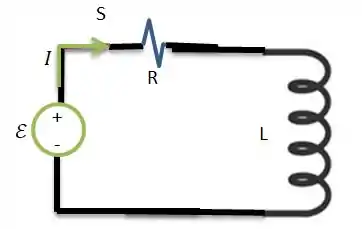
Surge no circuito uma corrente que pela Lei das Malhas de Kirchhoff gera queda de tenção no resistor () e no indutor ()...
Se lembrando de que a tensão em cima de um indutor é ...
Bem, então temos que encontrar a corrente através dessa equação e depois, como queremos a expressão para a tensão em cima do indutor (), bastará derivar e multiplicar por ...
Passo 2
Então vamos lá! Vamos primeiro resolver a EDO...
Repare que podemos dar uma arrumada nessa EDO...
E ARRA! Essa é uma EDO típica Linear de primeira ordem:
Onde a solução pode ser encontrada pela fórmula do fator integrante F...
A fórmula solução de acordo com as nossas técnicas de solução de EDO linear será então...
Como a integral de exponencial é ...
Simplificando então...
POW! é uma constante que surge da solução da EDO e que sempre pode ser encontrada sabendo uma condição inicial. No nosso caso, por exemplo, sabemos que no tempo , a corrente que atravessa o indutor é porque é exatamente quando a chave se fecha, saca?
Então...
Portanto, a corrente que circulará no circuito vai ser...
Passo 3
Para encontrar então, de acordo com o passo 1...
Derivando...
Outra forma de falar isso é...
Resposta
Letra C