Uma espira circular de área é atravessada por um campo magnético uniforme que oscila periodicamente no tempo. Considere que a dependência temporal dos campos (curva cheia) e (curva pontilhada) ilustrados nas figuras abaixo.
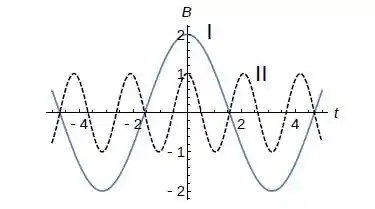
A máxima e o fluxo máximo de campo magnético se dão, respectivamente, nas situações
e .
e .
e .
e .
Para determinarmos a máxima e o fluxo máximo precisaríamos conhecer a resistência oferecida pelas espiras.
Passo 1
Analisando os gráficos, podemos notar algumas coisas. A primeira delas é que a equação dos campos terão mais ou menos essa cara:
Onde e . Logo:
Além disso, podemos relacionar as frequências e através dos períodos dos gráficos.
Portanto:
Agora podemos trabalhar.
Passo 2
A induzida é proporcional à variação do fluxo magnético. Mas como a área é constante, a induzida será proporcional à variação do campo magnético.
Sendo assim:
Assim, .
Logo, o gráfico representa a máxima.
Passo 3
O fluxo magnético é proporcional ao campo magnético, logo:
Assim, .
Logo, o gráfico representa o fluxo magnético máximo.
A resposta certa é a letra .
Resposta
e .