Uma lanterna comum possui duas pilhas, cada uma delas com uma fem , conectadas em série com uma lâmpada com resistência .
- Desprezando a resistência interna da pilha, qual é a potência fornecida para a lâmpada?
- Se a pilha se descarrega em , qual é a energia total fornecida para a lâmpada?
Passo 1
Para a gente resolver esse exercício, precisamos lembrar que a função que as pilhas exercem, como você já sabe lá do controle remoto da TV da sua casa, é fornecer energia para um circuito que faz o controle funcionar. No caso da lâmpada da lanterna é a mesma coisa: ela recebe uma energia, que é transportada pela corrente, que é utilizada para o seu funcionamento.
Então, a gente pode representar as duas pilhas ligadas em série com a lâmpada como seguinte circuito elétrico:
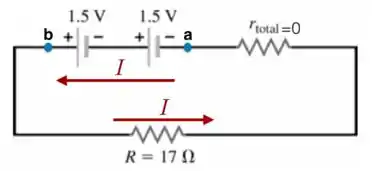
No caso da figura acima, as pilhas, ou baterias, não possuem resistência interna total , a energia por unidade de carga, a fem , que cada uma delas fornece é de e a resistência da lâmpada é . A corrente está no sentido anti-horário, como indicado em vermelho na figura acima.
Passo 2
a) Já que as duas pilhas juntas possuem uma fem total de , precisamos apenas encontrar a qual é a corrente que percorre o circuito fechado acima, pois a potência fornecida pelas pilhas é escrita como
Bom, na figura, supomos que a corrente circula no sentido anti-horário, como a gente mostrou lá. Do ponto para o ponto , temos dois aumentos de potencial, resultando em , já que nesse sentido, estamos indo do pólo para o pólo através das duas baterias. Confere? Dá uma checada nisso lá na figura.
Agora, quando a corrente passa pelo resistor da lâmpada, ocorre uma queda de potencial igual a . Quando a corrente volta para o ponto lá da figura, a soma das diferenças de potencial tem que ser igual a ZERO.
O que eu tô querendo te dizer para você com esses dois parágrafos anteriores é o seguinte:
Fechou agora, né? Colocando esse valor da corrente dentro de , a gente encontra
Daí você me pergunta: “O que significa esse valor?” Daí eu te respondo o seguinte: “Que bom que você está atento e perguntou, já estava esperando essa pergunta ….” Rsrs. E te digo: “ significa que 0,531 Joules de energia a cada segundo são fornecidos pelas pilhas para a lâmpada”. Sabendo disso, partamos para o próximo item…
Passo 3
- Como as pilhas fornecem para a lâmpada, a energia total das pilhas que vai embora em é:
Essa é a energia total perdida pelas pilhas. \0/
Resposta
- ;
- .