A figura mostra os fasores para três circuitos série com uma senoidal de frequência . A alternativa correta que estabelece a relação entre e (frequência de ressonância) em cada circuito é:
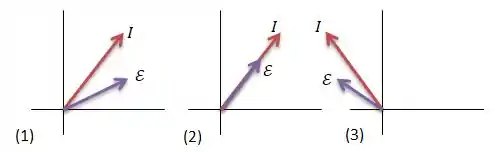
- Circuito (1); ; Circuito (2); ; Circuito (3), ;
- Circuito (1); ; Circuito (2); ; Circuito (3), ;
- Circuito (1); ; Circuito (2); ; Circuito (3), ;
- Circuito (1); ; Circuito (2); ; Circuito (3), ;
- Circuito (1); ; Circuito (2); ; Circuito (3), ;
Passo 1
Pow! Antes de passar para a análise de , vamos fazer algumas considerações iniciais pode ser?
Bem... No circuito , observamos que a corrente está na frente da , isto é, ela está adiantada. E o que isso significa em termos de circuitos?
Significa que o circuito tem um caráter mais capacitivo que reativo, ou seja, a reatância capacitiva () é maior que a reatância indutiva ():
E o mais interessante é que essas duas reatâncias são conhecidas em termos da frequência angular :
E é através disso que vamos analisar quanto , saca?
Passo 2
Para o circuito então...
OPA! De acordo com a nossa teoria quem é ?
SIM! É a frequência angular fundamental! Ou seja, é ! Então, para o circuito ...
Passo 3
Seguindo o mesmo raciocínio para os demais circuitos...
- Circuito 2:
- Circuito 3:
Resposta
Letra B.