Uma onda sonora se propaga até encontrar uma parede, refletindo e produzindo eco. Uma pessoa posicionada a da parede não ouve nenhum som. Ao caminhar em direção à parede, em linha reta e perpendicular à mesma, ela percebe o som proveniente da onda sonora, mas após se mover ela deixa de ouvir qualquer som novamente. Qual o comprimento da onda sonora original?
Passo 1
Cara... Vamos tentar imaginar o que está acontecendo, beleza?
Temos aqui uma pessoa parada a metros e ela não consegue perceber o som que está saindo de um auto falante externo...
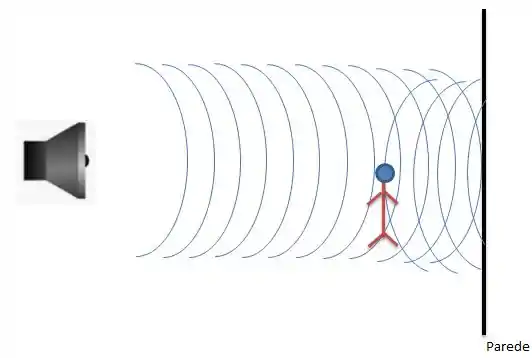
O enunciado nos disse que a pessoa onde ela se encontra, ela não escuta nenhum som, isso porque a pessoa se encontra exatamente num ponto de destruição total das ondas, onde a crista de uma encontra com o vale da outra (no desenho, a crista da onda refletida se encontra com o vale da onde emitida na cabeça do boneco).
OBS: Lembre-se de que nos desenhos, a crista sempre é a linha, o vale será exatamente o meio do espaço em branco.
Mas repare que, quando a pessoa se desloca, até ela encontrar outro ponto de destruição total, ela vai ter andado ...
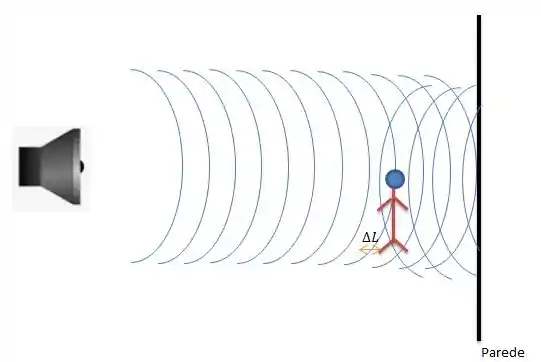
E esse deslocamento é chamado justamente o caminho entre dois mínimos de interferência, ta ligado? No nosso caso, a pessoa andou , até encontrar o outro ponto onde ela não escuta nada (o outro mínimo de interferência).
Passo 2
Tá, mas no que essa informação pode ser útil para a solução do nosso problema?
ORA! Sabemos pela teoria que a diferença de fase entre uma onda original e a mesma onda refletida em um objeto sempre pode ser dado por...
Onde é a diferença de caminho entre a onda original e a refletida. Só que a diferença de fase entre dois mínimos é sempre :
No nosso caso, a pessoa atinge essa diferença entre dois mínimos após andar , então podemos dizer que essa é a diferença de caminho entre dois mínimos no nosso caso, ou seja... . Então...
Resposta
Letra D.