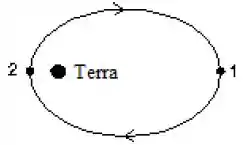
A figura mostra um satélite numa órbita elíptica em torno da Terra. Se denota o módulo do momento angular do satélite e denota a sua energia cinética, é correto afirmar que nas posições 1 e 2,
(A) e
(B) e
(C) e
(D) e
(E) e
Passo 1
O momento angular só varia se houver algum torque externo sobre o sistema.
Como não há forças externas atuando sobre o sistema (sistema isolado), não há torques externos.
Assim, temos que o momento angular se conserva. Logo:
Passo 2
E para achar uma relação entre as energias cinéticas, precisamos olhar para as velocidades.
A ideia é que quanto mais perto da Terra o satélite estiver, maior será sua velocidade.
Mas por que?
Podemos achar isso a partir da expressão anterior.
O momento angular de uma “partícula” é dado por:
Dá uma olhada nos vetores posição e velocidade :
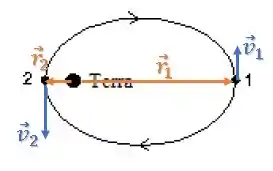
Nos dois casos eles são perpendiculares, então:
Passo 3
Bom, se o momento angular se conserva:
Como a distância é maior que a distância , o termo dá maior que 1.
Temos, então, que a velocidade é maior que a velocidade .
Consequentemente:
Novamente, quanto mais próximo o satélite estiver da Terra, mais rápido ele estará.
Resposta
Letra (E)