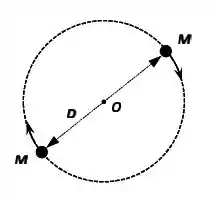
Um sistema binário é composto por duas estrelas de massas M iguais, separadas por uma distância D, descrevendo órbitas circulares em torno do centro de massa O do sistema, conforme a figura abaixo.
Determine o período T das órbitas em função de G, M, e D e verifique a terceira Lei de Kepler.
Obtenha a energia total do sistema em termos de G, M, e D.
Passo 1
Como as estrelas estão em um movimento circular uniforme, temos que a força gravitacional é igual a força centrípeta.
Vamos escrever a força centrípeta em função do período, e para isso vamos substituir a velocidade pela velocidade angular e escrever a velocidade angular em função do período. Da seguinte forma:
Igualando as forças temos:
Antes de passar a raiz quadrada dos dois lados, vamos verificar a 3ª Lei de Kepler. Lei das proporções que diz que
Bem a lei nesse caso é confirmada, encontramos que é proporcional ao cubo da distância e inversamente proporcional a massa .
Agora sim, vamos passar a raiz dos dois lados e encontrar
Passo 2
Agora a energia total do sistema vai ser a soma da energia de interação entre as estrelas somada com a energia cinética de cada uma
A energia de interação entre as estrelas vai ser (lembrando que a distância entre as duas é )
Passo 3
Já as energias cinéticas das estrelas vão ser iguais
A velocidade de cada estrela vai ser o comprimento da trajetória dividido pelo período da órbita
Como já calculamos o período essa conta fica mole!
Voltando pra nossa energia cinética
Passo 4
Assim a nossa energia total será
Resposta
A)
B)