[Questão 11]
A figura ao lado mostra um foguete de massa que descreve uma órbita elíptica em torno da Terra, onde é a distância da Terra em relação ao centro da elipse e é o semi-eixo maior da elipse. A massa da Terra é . A única força que atua sobre o foguete é a atração gravitacional do planeta. No ponto A, o foguete tem velocidade de módulo . Com base nessas informações, responda as questões 11, 12 e 13.
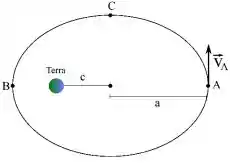
Usando os seus conhecimentos sobre torque e momento angular, determine o módulo da velocidade do foguete no ponto .
(A)
(B)
(C)
(D)
(E) Não é possível calcular com os dados fornecidos.
Passo 1
Trajetória elíptica... queremos calcular a velocidade no ponto .
Mas que coisa complicada de se fazer nessa trajetória estranha aí, né?
Mas, repara que ele deu uma dica, “usando seus conhecimentos de torque e momento angular”.
Como a gente pode usar esses conceitos?
Como o satélite está orbitando ao redor da terra, podemos usar ela como referencial para calcular o momento angular do satélite.
Mas por que fazemos isso?
Simples, olha para a força gravitacional sobre o satélite:
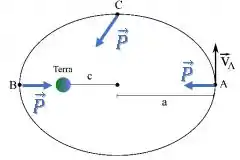
A força gravitacional sempre aponta para a Terra.
Então, se considerarmos o eixo de rotação passando por ela, a força peso nunca gera torque, pois aponta na direção desse eixo de rotação:
Ahhhh, agora temos um ponto importante...
Se o sistema está livre de torques externos, o momento angular se conserva:
Então, considerando a Terra como referencial, podemos conservar o momento angular do satélite, assim, podemos igualar os momentos angulares em quaisquer pontos da órbita, como por exemplo o ponto A e B:
Com isso, conseguimos relacionar as velocidades e .
Passo 2
Vamos achar que são esses momentos angulares.
O momento angular de uma partícula é dado por:
Temos os seguintes vetores e para os pontos A e B:
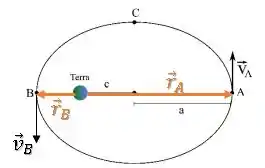
Como os vetores e são perpendiculares nos dois casos, temos que o módulo do momento angular é:
Então, temos:
Conservando o momento angular dos dois, temos:
Assim, a velocidade será:
Passo 3
Quem são esses raios e ?
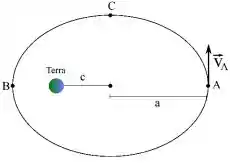
A distância da Terra ao ponto A é:
A distância da Terra ao ponto B será a distância do centro da elípse ao lado B menos a distância do centro da elípse à Terra :
Passo 4
Substituindo esses valores, temos:
Ficamos com a letra (D).
Resposta
Letra (D)