Um satélite está em órbita circular equatorial geossíncrona, isto é, visto da Terra ele permanece estacionário num ponto fixo acima do equador. Qual das afirmações abaixo a respeito desse satélite é verdadeira?
(A) Há somente uma força agindo sobre o satélite.
(B) Há duas forças agindo sobre o satélite, e sua resultante é zero.
(C) Há duas forças agindo sobre o satélite, e sua resultante não é zero.
(D) Há três forças agindo sobre o satélite.
(E) O satélite pode ter qualquer período.
Passo 1
Fala aí galera, tudo bacana com vocês? Bora cair pra cima da questão. Bem, ela começa com esse termo bem excêntrico aí (órbita circular equatorial geossíncrona), que nada mais significa que esse satélite (na visão do observador) está “parado” no céu, pois ele orbita a terra no mesmo período que a terra orbita o próprio eixo. Daí vem o nome “geossíncrona”, que significa que é a orbita em que os corpos nessa distância rotacionam de forma síncrona com a terra.
Passo 2
Indo pros itens, vamos analisar qual é o verdadeiro. Começando no item a):
(A) Há somente uma força agindo sobre o satélite.
Bem, você sabe como a gente acha as forças que agem no corpo do satélite? Vamos lembrar da fórmula da atração gravitacional. Usaremos ela porque a gente quer entender que forças agem sobre o satélite. Ela é dada por:
Para a seguinte situação:
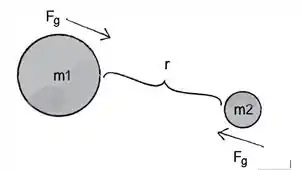
No caso da nossa órbita, apenas a gravidade atua nela. Pois ela está estacionaria em relação a , significando que nenhuma outra força age sobre ela. Portanto, item a) verdadeiro!
Passo 3
Como provamos que apenas uma força age sobre o satélite, todos os outros itens são falsos e não vale a pena a gente conversar muito sobre. Mas no item e) porque ele é falso? Pois bem, como mostrado no passo 1, ele não pode ter qualquer período. Tem que ser o mesmo período da terra (um dia) .