UNICAMP-Física 2-P1-2020.2
Questão 1
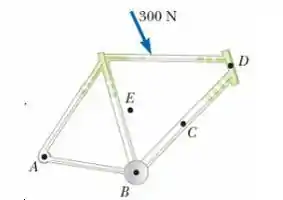
Uma força de 300 N é exercida sobre o quadro de uma bicicleta, com mostrado na figura. Considere o torque exercido por essa força em torno de eixos perpendiculares ao plano do papel que passam por cada um dos pontos de A a E , sendo E o centro de massa do quadro. Considere como positivos os torques que provocam rotação no sentido anti-horário. Ordene os torques 
do maior para o menos, notando que zero é maior que uma quantidade negativa.
Passo 1
Fala galerinha tranquilidade, essa é uma questão de análise, isso porque a única quantidade que temos conhecimento é a força externa de 300 N indicada na figura, então com base nisso temos que avaliar o torque resultante em cada um dos pontos. Para isso vamos utilizar a definição de torque. Que é:
Passo 2
Nesse ponto o que vamos fazer é prolongar a força externa F, com isso nós vamos traçar o que seriam os ângulos entre a força e o braço de alavanca, considerando que o movimento de rotação é em torno do ponto E. E o resultado é mostrado no desenho abaixo.
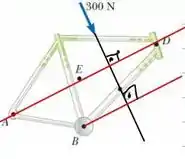
Passo 3
Passo 4
Como o problema não diz qual a distância exata de cada ponto, o que podemos fazer é fazer uma análise visual e identificar quais são maiores.
Considerando essas informações, o que podemos fazer agora é identificar os maiores braços. Resultando.
Agora você pode se perguntar se o torque no ponto C, nesse ponto o torque é zero, pois ele está na mesma direção que a força, um produto vetorial é zero nesse caso. Onde ele entraria? Nesse caso estamos considerando os torques a esquerda do ponto E negativos, logo o ponto C sendo zero entre logo depois do maior torque que é o do ponto D.
Resposta
A alternativa que descreve os torques é a A.