Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Coeficientes Indeterminados – Produto de Funções

Ver Teoria
Exercício 15123456789101112131416171819

Enunciado

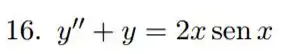
Passo 1

Lá vamos nós resolver mais uma EDO não homogênea. Precisamos reoslver

y ' ' + y = 2 x sen ⁡ ( x )

O jeito aqui é primeiro ignorar a parte à direita da equação e resolver a EDO como se fosse homogênea.

y ' ' + y = 0

Encontrando a equação característica

r 2 + 1 = 0

Determinamos as raízes

r = ± i

E a solução homogênea é

y h x = C 1 cos ⁡ x + C 2 sen ⁡ x

Passo 2

Agora sim vamos começar a trabalhar com aquele lado direito. Temos do lado direito

2 x sen ⁡ ( x )

Nesse caso, é um produto de duas funções, então precisamos “chutar” uma solução para cada função e a solução particular será o produto entre elas.

y p 1 = a x + b

Atenção que as funções seno e cosseno já apareceram na solução homogênea, então

y p 2 = c x sen ⁡ x + d x cos ⁡ x

Fazendo o produto entre as soluções

y p = a x + b   c x sen ⁡ x + d x cos ⁡ x

y p = a x 2 sen ⁡ x + b x 2 cos ⁡ x + c x sen ⁡ x + d x cos ⁡ x

Passo 3

Para encontrar as constantes a , b , c   e   d precisamos derivar a solução que chutamos e aplica-la na EDO.

y p = a x 2 sen ⁡ x + b x 2 cos ⁡ x + c x sen ⁡ x + d x cos ⁡ x

y p ' = 2 a x sen ⁡ x + a x 2 cos ⁡ x + 2 b x cos ⁡ x - b x 2 sen ⁡ x + c sen ⁡ x + c x cos ⁡ x + d c o s   x - d x sen ⁡ x

y p ' = x sen ⁡ x 2 a - d + x cos ⁡ x 2 b + c + a x 2 cos ⁡ x - b x 2 sen ⁡ x + c sen ⁡ x + d cos ⁡ x

Derivando novamente

y p ' ' = sen ⁡ x 2 a - d + x cos ⁡ x 2 a - d + cos ⁡ x 2 b + c - x sen ⁡ x 2 b + c + 2 a x cos ⁡ x - a x 2 sen ⁡ x - 2 b x sen ⁡ x - b x 2 cos ⁡ x + c cos ⁡ x - d sen ⁡ x

y p ' ' = sen ⁡ x 2 a - 2 d + x cos ⁡ x 4 a - d + cos ⁡ x 2 b + 2 c + x sen ⁡ x - 4 b - c - a x 2 sen ⁡ x - b x 2 cos ⁡ x

Aplicando na EDO

y ' ' + y = 2 x sen ⁡ ( x )

sen ⁡ x 2 a - 2 d + x cos ⁡ x 4 a - d + cos ⁡ x 2 b + 2 c + x sen ⁡ x - 4 b - c - a x 2 sen ⁡ x - b x 2 cos ⁡ x + a x 2 sen ⁡ x + b x 2 cos ⁡ x + c x sen ⁡ x + d x cos ⁡ x = 2 x sen ⁡ x

Resolvendo essa coisa gigantesca ficamos com

a = 0

b = - 1 2

c = 1 2

d = 0

Então

y p x = - x 2 2 cos ⁡ x + x 2 sen ⁡ ( x )

Passo 4

Sabemos que

y x = y h x + y p ( x )

E

y h x = C 1 cos ⁡ x + C 2 sen ⁡ x

y p x = - x 2 2 cos ⁡ x + x 2 sen ⁡ ( x )

Então

y x = C 1 cos ⁡ x + C 2 sen ⁡ x - x 2 2 cos ⁡ x + x 2 sen ⁡ ( x )

Resposta

y x = C 1 cos ⁡ x + C 2 sen ⁡ x - x 2 2 cos ⁡ x + x 2 sen ⁡ ( x )

Exercícios de Livros Relacionados

Nos problemas 1-32, resolva a equação diferencial dada pelo método dos coeficientes indeterminados.16. y ' ' + 3 y ' - 10 y = x e x + 1
Nos problemas 1-32, resolva a equação diferencial dada pelo método dos coeficientes indeterminados.21. y ' ' + 25 y = 20 s e n5 x
Em cada um dos problemas de 21 a 28:Determine uma forma adequada para Y(t) para usar o método dos coeficientes indeterminados. Use um sistema de álgebra computacional para encontrar uma solução partic
Em cada um dos problemas de 21 a 28:Determine uma forma adequada para Y(t) para usar o método dos coeficientes indeterminados. Use um sistema de álgebra computacional para encontrar uma solução partic
Em cada um dos problemas de 21 a 28:Determine uma forma adequada para Y(t) para usar o método dos coeficientes indeterminados. Use um sistema de álgebra computacional para encontrar uma solução partic