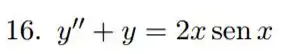Exercícios de Método dos Coeficientes Indeterminados – Produto de Funções - Lista de Exercícios Resolvida

A EDO possui uma solução geral da forma:

(a)

(b)

(c)

(d)

(e)

Resolva a EDO

Seja a equação diferencial ordinária .

1. Considere . Encontre a solução geral desta equação diferencial ordinária.
2. Considere, agora, que , e . Encontre a solução para este problema de valor inicial.

Resolva o problema de contorno:

Resolva o problema de contorno:

Determine a solução geral da equação

Determine a solução geral da equação diferencial linear de 2ª ordem não-homogênea com coeficientes constantes:

Dica: Transforme a equação para , como na 1ª questão.

Encontre todas as soluções da EDO:

1. Determine a solução geral da equação
2. Utilize o resultado do item (a) para determinar a solução geral da equação
3. Utilize o resultado do item (b) para determinar a solução do problema de valor inicial

Qual o valor de de modo que nenhuma solução particular da equação diferencial

Seja da forma , para alguns .

5. Nenhuma das alternativas

A EDO possui uma solução geral da forma:

(a)

(b)

(c)

(d)

(e)

Considere a equação de segunda ordem não-homogênea

Pelo método dos coeficientes indeterminados, existe uma solução da equação da forma onde é um polinômio. O grau de é

Escolha uma:

Determine a solução geral da equação diferencial linear de 2ª ordem não homogênea com coeficientes constantes:

Resolva os seguintes problemas de valor inicial:

1.

2.

3.

Seja a equação diferencial ordinária .

1. Considere . Encontre a solução geral desta equação diferencial ordinária.
2. Considere, agora, que , e . Encontre a solução para este problema de valor inicial.

Determine a solução geral da equação

A EDO possui uma solução da forma:

Nenhuma das demais alternativas