Uma pessoa puxa um sistema formado por 2 blocos que encontra-se apoiado sobre uma mesa

horizontal. O sistema está inicialmente em repouso a uma distância em relação a borda da mesa. O coeficiente de atrito cinético entre o bloco A e a mesa é , enquanto o coeficiente de atrito estático entre os blocos A e B é . As massas dos blocos são . Considerando que a força é aplicada sobre o bloco A em uma direção que faz um ângulo de com a horizontal e adotando .

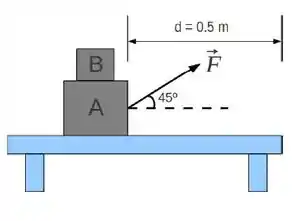
1. Calcule o máximo valor da força para o qual o bloco B se move junto com o sistema sem deslizar.
2. Calcule o trabalho total realizado por esta força (em seu valor máximo) para mover o sistema até a borda da mesa.
3. Calcule a potência média fornecida pela pessoa para mover o sistema até a borda da mesa na condição acima.
4. Qual o valor da potência instantânea quando o sistema alcança a borda da mesa?

a)

Pois bem, galera! Acho que a primeira coisa que a gente faz quando vê uma questãozinha assim é isolar as forças. Sem pensar muito, teremos:

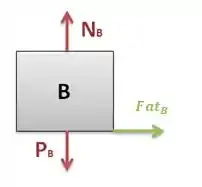
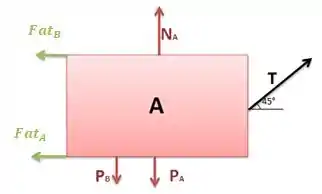
Note que temos aqui um caso de 3ª Lei de Newton!

A força de atrito em B (), é feita pelo bloco A, e por isso, tem uma força de reação que atua no bloco A, com mesmo módulo e sentido contrário a que atua no bloco B.

Se liga! Quando o bloco B estiver na iminência de entrar em movimento relativo com o bloco A a força de atrito estático será máxima, e assim poderá ser calculada por .

Fazendo as equações de Newton para esses sistemas, teremos:

Bloco B:

Forças Verticais:

Forças Horizontais:

Como a gente sabe que vai sobrar:

Bloco A:

Forças Verticais:

NÃO ESQUECER DA COMPONENTE VERTICAL DA FORÇA T!!!

Forças Horizontais:

Como a gente viu lá no Bloco B, . Substituindo nessa nossa última equação, teremos:

Vamos aproveitar que ele nos deu os valores de algumas incógnitas e substituir logo pra não ficar tão confuso a forma algébrica.

Fazendo isso também para a equação que achamos para as forças verticais para o bloco A, vai ficar:

Vamos ter um sisteminha linear com duas equações e duas incógnitas, são elas:

Como a gente quer achar aqui o valor de T, vamos isolar o da primeira equação, substituir na segunda e pronto! Acabou-se.

b)

Molezinha! A gente sabe que o trabalho pode ser calculado por:

Comos a gente já tem todas as incógnitas é só substituir!

c)

Para calcular a potência em qualquer situação, basta utilizar a formulitxa:

Já achamos o W, porém não temos o , mas é facílimo de descobrir. A gente sabe a aceleração e também sabemos o quanto ele vai andar até chegar na ponta de mesa que é . Daí é só usar:

Substituindo lá na potência, e matando a letra c, teremos:

d)

Potência Instantânea! Quando eu ouço essas paradas com “instantânea” logo me lembro de derivada e , até porque o é um período infinitesimal de tempo, ou seja, um instante. Vamos tentar achar relações com derivadas aqui, como por exemplo usando a fórmula do trabalho.

Sendo um deslocamento qualquer no eixo x.

Para deslocamentos tão pequenos sendo considerados também teremos um trabalho bem pequeno podendo ser considerado , e assim teremos:

Ah! Aqui que está o pulo do gato lá dos . Dividindo de ambos os lados por , teremos:

Sabemos que e que , e então vai ficar...

Para aniquilar de vez essa questão, basta agora achar qual velocidade o bloco vai chegar na ponta da mesa, o que não é difícil!

Como já sabemos que ...

Como nossa força é a tração que resulta movimento no eixo x, ela nada mais é que