Um piano de massa está no primeiro andar de um prédio, a uma altura . Pretende-se descer o piano suavemente para o térreo sobre um plano inclinado de comprimento , conforme a figura ao lado. Uma corda realiza uma tração sobre o piano. Considere que o piano desce com velocidade constante e entra em repouso ao chegar no solo, e que .
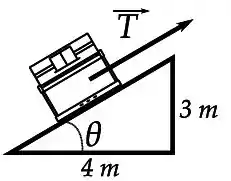
(a) Desconsiderando o atrito com o solo, determine o trabalho total realizado pela tração .
(b) Desconsiderando o atrito com o solo, determine a potência que deve ser aplicada na corda para descer o piano com uma velocidade .
(c) Sabe-se que o coeficiente de atrito cinético entre o piano e o solo é . Considerando o atrito com o solo, determine a potência que deve ser aplicada na corda para descer o piano com uma velocidade .
Passo 1
Para resolver essa questão, vai ser bem útil analisar as forças atuando sobre o piano. Então, vamos começar com o Diagrama do Corpo Livre.
Como, inicialmente, não há atrito, temos apenas uma força peso para baixo e uma força normal perpendicular ao plano, além da força de tração :
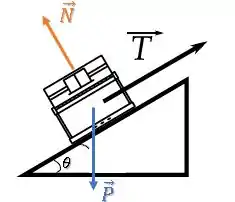
Para facilitar a nossa vida, vamos decompor essa força peso nas componentes paralela e perpendicular à rampa:
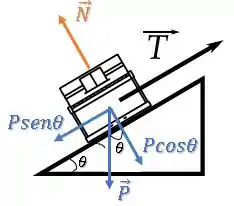
Qual a ideia?
Se o piano desce com velocidade constante, é porque essa força de tração está equilibrando a componente da força peso que puxa o piano para baixo da rampa.
Ou seja, o piano está em equilíbrio e não vai ter nenhuma aceleração.
Vamos aos itens.
Passo 2
Na letra (a), queremos o trabalho realizado pela força de tração ao longo desse deslocamento.
O trabalho da força vai ser dado pelo produto escalar entre esse vetor e o vetor deslocamento :
Como a força de tração é constante ao longo do deslocamento, podemos simplesmente calcular esse produto escalar com:
Onde é o ângulo entre os dois vetores.
O vetor deslocamento vai ser na direção da rampa para baixo , enquanto a tração está na direção da rampa para cima:
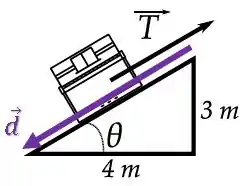
Como os vetores estão em sentidos opostos, o ângulo entre eles é:
Assim, o trabalho da força será negativo:
Sabemos que o valor do deslocamento foi de , porém, quanto vale essa força de tração ?
Passo 3
Podemos encontrar a força de tração através do equilíbrio de forças do piano:
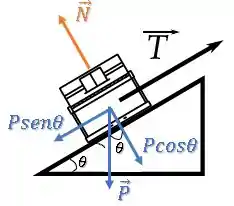
Sabemos a massa e a gravidade , já esse podemos encontrar a partir da geometria da rampa:
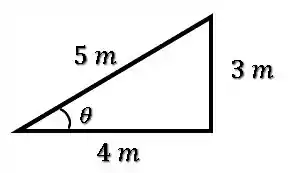
Substituindo os valores na expressão para , temos:
Passo 4
Agora, que encontramos o valor de , o trabalho dessa força será:
Ou então:
Passo 5
Na letra (b), queremos a potência aplicada na corda, sabendo que a velocidade do piano é de .
A potência diz em quanto tempo está sendo realizado um certo trabalho, sendo trabalho uma forma de energia.
Então, a potência vai ser nada mais, nada menos que:
Acabamos de calcular o trabalho , mas ainda falta saber quanto tempo durou o deslocamento .
Passo 6
Como sabemos a velocidade e a distância percorrida , basta jogarmos na fórmula:
Passo 7
Pronto, agora, conseguimos calcular a potênica:
Passo 8
Na letra (c), agora, vamos considerar uma força de atrito cinética com coeficiente e queremos a nova potência aplicada na corda para descer o piano com a mesma velocidade de .
Como fica a nova configuração de forças?
Como a força de atrito atua contrária ao deslizamento do piano, teremos:
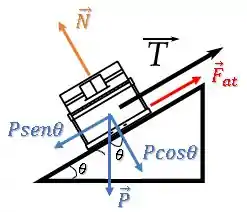
Então, a nova força de tração necessária para equilibrar o piano e não deixar ele descer a rampa com uma aceleração é:
Já sabemos temos todos esses dados, exceto a força normal .
Passo 9
Para achar a força normal, basta fazer o equilíbrio de forças na direção perpendicular à rampa:
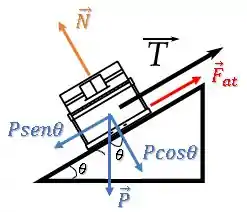
Substituindo isso na expressão da força de tração:
Passo 10
Então, o trabalho será:
Assim, podemos calcular a potência:
Como a velocidade é a mesma , já vimos no Passo 6, que o piano leva nesse deslocamento.
Além disso, podemos tirar tanto o seno quanto o cosseno de :
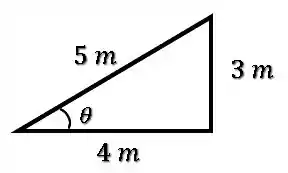
Assim, a potência será:
Fazendo essa conta, chegamos em:
Resposta
(a)
(b)
(c)