USP, Probabilidade, P2-2019.2, Teste 15
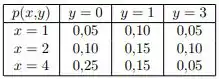
15) Um shopping de São Paulo possui um supermercado e uma farmácia. Sejam as variáveis aleatórias e que representam o número de vezes que um cliente assíduo desse shopping faz compras no supermercado e na farmácia durante um mês, respectivamente. A distribuição de probabilidade conjunta está na tabela abaixo. O valor médio do número de vezes que um cliente faz compra no supermercado dado que comprou vezes na farmácia vale:
A)
B)
C)
D)
E)
Passo 1
Faaaala galerinha, todo mundo animado pra matar mais uma questão de probabilidade?
Esse exercício traz uma distribuição conjunta de duas variáveis aleatórias discretas e . Basicamente, devemos determinar o valor esperado, ou média, de dado que .
Sei que vocês já estão ligados como calcular valor esperado de uma V.A discreta, é só fazer:
Mas, e quando temos uma probabilidade condicionada a um valor fixo de , por exemplo. Como podemos calcular a esperança?
Então, nesse caso só precisamos adaptar um pouco a probabilidade na fórmula da esperança. Ficamos com:
Massa! Então, bora atrás desses valores.
Passo 2
Pra começar, precisamos relembrar como calculamos probabilidade condicional:
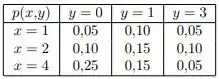
Pela tabela dada, na última coluna da direita, vale que:
Assim, usando nossa expressão para a probabilidade condicional, temos que:
Muito bom! Estamos quase lá.
Passo 3
Beleza, agora que já temos as probabilidades condicionais é só substituir na fórmula da esperança e correr pro abraço!
Prontinho 😊
Espero que vocês tenham entendido bem, até a próxima 😉
Resposta
Letra C: