Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.
- Obtenha a distribuição conjunta de e através de uma tabela e diga se e são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de e de . Em seguida, obtenha e . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
Passo 1
(a)
A gente tem que montar nossa tabela marota.
Primeiro vamos entender melhor o problema.
pode assumir os valores: 0(se não sair nenhuma branca nas duas), 1 ou 2.
Bom, vamos seguir os conselhos do exercício.
Passo 2
Vamos começar com as distribuições marginais.
Começando por .
Já que são 2 bolas vermelhas, num total de 5 bolas.
Já que são 3 bolas brancas, num total de 5 bolas.
Passo 3
Agora vamos fazer a distribuição marginal de .
Já que pra não sair nenhuma bola branca, na primeira retirada tem que sair uma vermelha, , e na segunda também tem que sair uma vermelha, (lembrando que é sem reposição).
Pra sair no total 1 branca, temos duas opções: sair branca na primeira (3/5) e vermelha na segunda (2/4) ooou sair vermelha na primeira (2/5) e branca na segunda (3/4).
Pra finalizar.
Pra sair 2 brancas, tem que sair uma branca na primeira (3/5) e uma branca na segunda (2/4).
Passo 4
Seguindo os conselhos do exercício, vamos calcular agora:
Probabilidade de sair bola branca na primeira retirada e no total não sair nenhuma branca. HAM? Impossível, concorda?
Então:
Agora calcular,
Também é impossível, certo? Não dá pra sair duas bolas brancas se na primeira retirada sair uma vermelha. Então:
Passo 5
Vamos montar a tabela com os valores que a gente já tem.
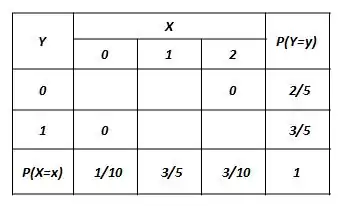
Completando a tabela, lembrando que o somatório das linhas e das colunas tem que ser igual aos valores da distribuição marginal, a gente ficará com:
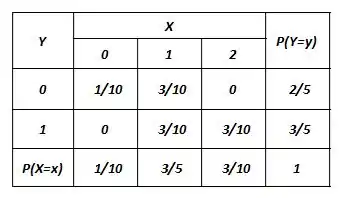
Pronto, era isso que a gente queria.
Passo 6
Agora pra ver se são independentes é ver se existe algum caso que não verifique a seguinte afirmação.
Nesses casos é bom olhar pra exemplos que tenham 0 na tabela, fica mais tranquilo verificar. Por exemplo:
Então,
E com isso dizemos que e não são independentes.