Sejam e duas v.a.’s discretas cuja função de probabilidade conjunta é expressa por:
Determine a constante para que seja uma função de probabilidade das variáveis aleatórias e .
Passo 1
Bom, para que a função seja uma função de probabilidade, a soma das probabilidades das distribuições marginais deve ser igual a 1. Isto é,
Confuso né? E então, o que precisamos fazer?
Vamos começar assumindo que a nossa é uma função de probabilidade conjunta. Agora que assumimos isto, vamos montar uma tabela para descrever os valores de nossa . Mas calma, até qual valor de e iremos montar a tabela? Porque pelo enunciado da questão eles variam de 3 até infinito.....
E aí??????? Bom, vamos montar até o valor 5, depois vocês irão perceber que é desnecessário continuar.
Portanto, temos a seguinte tabela:

Vocês conseguem perceber que a cada vez que a gente aumenta o valor de ou de o denominador fica maior? Consequentemente, o número final fica cada vez menor. É por causa disso que podemos parar por aqui no cálculo.
Passo 2
Agora que calculamos o valor da probabilidade de cada uma das combinações de e para valores de e variando entre e , o que precisamos fazer agora? A resposta para esta pergunta é: precisamos determinar dois parâmetros que a questão nos deu: as distribuições marginais e .
A ideia por trás da distribuição marginal é simples. Lembra que estamos com uma distribuição conjunta ? Então, imagina aí: o que aconteceria se a gente fixasse um determinado e variasse o ? Se somarmos todas essas probabilidades, obteríamos uma probabilidade deste nosso evento acontecer.
Pronto, esta é uma ideia resumida da distribuição marginal. Mas sim, o que importa é como calcular. E como fazemos isto? Aí já é mais fácil ainda! É só nós somarmos as linhas (colocando o resultado final na última coluna a direita) e somarmos as colunas (colocando o resultado final na última linha abaixo).
Por fim, é basicamente acrescentar uma linha e uma coluna a tabela dada na questão. Portanto, temos:
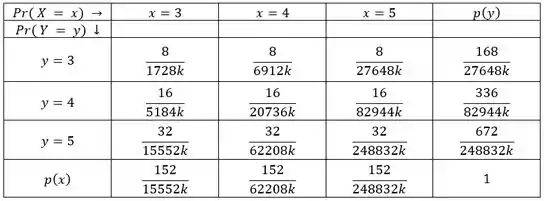
E agora? O que devemos fazer? Eu digo a vocês que a chave para resolvermos a questão continua na tabela. Em especial, na última linha e última coluna. Mais especial ainda naquele belo número 1.
Para que a nossa seja uma função de probabilidade, significa que a soma das probabilidades das distribuições marginais (aquela última linha e última coluna), tem que dar igual ao número 1.
Vamos utilizar a identidade acima para calcularmos o valor de . Portanto,
Então, basta descobrirmos qual o valor de que satisfaz a seguinte relação:
Portanto, o valor aproximado de que torna uma função de probabilidade de variáveis e é aproximadamente .