Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Discretas

Ver Teoria
Exercício 11123456789101213141516171819

Enunciado

Covariância e Correlação para V.a. Multidimensionais

b) Seja ( X , Y ) variável aleatória discreta com a seguinte distribuição de probabilidade conjunta:

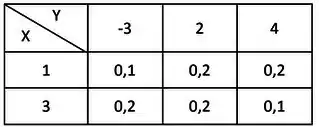
Pede-se:

Calcular C o v ( X , Y ) e o Coeficiente de Correlação ρ ( X , Y )

Observação:

- Demonstrar a expressão da Covariância.

- Mostre os resultados considerando 4 casas decimais.

Passo 1

Letra b)

Relembrando a fórmula da covariância:

C o v X , Y = E X Y - E X E Y

E antes de prosseguimos, vamos calcular as distribuições marginais de X e Y , somando os valores de mesma linha ou mesma coluna na tabela:

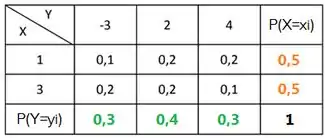
Agora vamos calcular as esperanças:

E X = 1 × 0,5 + 3 × 0,5 = 2

E Y = - 3 × 0,3 + 2 × 0,4 + 4 × 0,3 = 1,1

E X Y = 1 × - 3 × 0,1 + 1 × 2 × 0,2 + 1 × 4 × 0,2 + 3 × - 3 × 0,2 + 3 × 2 × 0,2 + 3 × 4 × 0,1 = 1 , 5

Aplicando na fórmula da covariância:

C o v X , Y = 1,5 - 1,1 × 2 = - 0,7

Passo 2

E agora o coeficiente de correlação, que tem a fórmula:

ρ X , Y = C o v ( X , Y ) σ X . σ Y

Onde esses σ são os desvios padrões de X e Y . Precisamos calcular então as variâncias, lembrando que:

V a r X = E X ² - E ( X ) ²

Calculando as esperanças ao quadrado:

E X ² = 1 ² × 0,5 + 3 ² × 0,5 = 5

E Y ² = ( - 3 ) ² × 0,3 + 2 ² × 0,4 + 4 ² × 0,3 = 9,1

Então as variâncias ficam:

V a r X = 5 - 2 2 = 1

V a r Y = 9,1 - 1,1 2 = 7,89

E os desvios-padrões:

σ X = 1 = 1

σ y = 7,89 = 2,8089

Então o coeficiente de correlação é:

ρ X , Y = - 0,7 1 × 2,8089 = - 0,2492

Resposta

C o v X , Y = - 0,7

ρ ( X , Y ) = - 0,2492

Exercícios de Livros Relacionados

Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número