Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Discretas

Ver Teoria
Exercício 91234567810111213141516171819

Enunciado

P1- UFRJ 2016.1 – Questão 04

Quando os consumidores abastecem seus carros em determinado posto de gasolina situado beira de uma estrada, eles sempre aproveitam para fazer também uma refeição no restaurante self-service desse posto. Cada vez que isso acontece:

(1) O carro só é abastecido com um tipo de combustível, a saber, só com gasolina ou só com álcool.

(2) 70% dos carros usam gasolina e 30% usam álcool. Seja W ∼ Bernoulli(p), com p = 0,7, onde W = 1 corresponde a gasolina e W = 0 corresponde a álcool.

(3) A quantidade X de combustível em litros (de gasolina ou de álcool) colocada no tanque do veículo é Normal com média μ x = 30 e desvio padrão σ x = 10 .

(4) O preço da gasolina é     α = 4   r e a i s / l i t r o e o preço do álcool é β = 3 r e a i s / l i t r o .

(5) A quantidade Y de comida, em quilos, consumida em uma refeição no restaurante é Normal com média µY = 0,5 e desvio padrão σY = 0,2.

(6) O preço da comida no restaurante é γ = 30 reais/quilo.

(7) Há independência entre as variáveis aleatórias W, X e Y .

Então, T = [αW + β(1 − W)]X + γY é o montante dos gastos em reais, com combustível e com alimentação, durante uma parada nesse posto de um consumidor selecionado aleatoriamente. Calcule:

a)A distribuição da despesa total T, dado que o carro é abastecido com gasolina

(b) A distribuição da despesa total T, dado que o carro é abastecido com álcool.

(c) A média e o desvio padrão dessa despesa total T (sem separar pelo tipo de combustível).

(d) A probabilidade de que ele gaste ao todo no máximo 150 reais, ou seja, P r ⁡ ( T ≤ 150 ) .

Sugestão: Use o Teorema da Probabilidade Total, condicionando em W.

Passo 1

Vamos entender o problema?

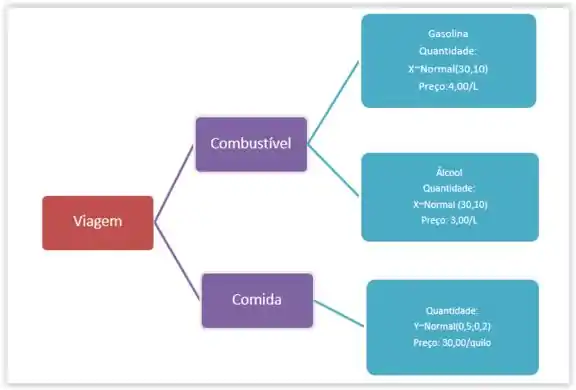
Olhando assim podemos entender melhor aquele T (montante). O gasto total será:

T = G a s t o   G a s o l i n a + G a s t o   Á l c o o l + G a s t o   C o m i d a

G a s t o   g a s o l i n a = P r o b a b i l i d a d e   d e   p o r   g a s o l i n a × Q u a n t i d a d e × P r e ç o

G a s t o   á l c o o l = P r o b a b i l i d a d e   d e   p o r   á l c o o l × Q u a n t i d a d e × P r e ç o

G a s t o   C o m i d a = Q u a n t i d a d e × P r e ç o

Assim

G a s t o   G a s o l i n a = W × X × α

G a s t o   Á l c o o l = 1 - W × X × β

G a s t o   C o m i d a = Y × γ

T = W × X × α + 1 - W × X × β + ( Y × γ )

Passo 2

Agora que já entendemos melhor o enunciado vamos para os itens...

a) A distribuição da despesa total T, dado que o carro é abastecido com gasolina

Como informado no enunciado (1) sabemos que se o carro é abastecido com gasolina ele não será abastecido com álcool, portanto

T = W × X × α + ( Y × γ )

Notamos que T é uma função de distribuições, ou seja, ela mescla (combinação linear) da distribuição normal da quantidade de gasolina e a distribuição normal da quantidade de comida.

Para definirmos uma distribuição precisamos da média e da variância da mesma, assim podemos falar que:

μ T = α μ X + γ μ Y

μ T = 4 × 30 + 30 × 0,5 = 135   r e a i s

σ T 2 = α 2 σ X 2 + γ 2 σ Y 2

σ T 2 = 4 2 × 10 2 + 30 2 × 0,2 2 = 1636   r e a i s 2  

Passo 3

(b) A distribuição da despesa total T, dado que o carro é abastecido com álcool.

Com um pensamento análogo a letra (a), faremos

μ T = β μ X + γ μ Y

μ T = 3 × 30 + 30 × 0,5 = 105   r e a i s

σ T 2 = β 2 σ X 2 + γ 2 σ Y 2

σ T 2 = 3 2 × 10 2 + 30 2 × 0,2 2 = 936   r e a i s 2  

Passo 4

(c) A média e o desvio padrão dessa despesa total T (sem separar pelo tipo de combustível).

Agora olharemos para a fórmula dada no enunciado/mostrada por nós:

T = W × X × α + 1 - W × X × β + ( Y × γ )

T = X × W × α + 1 - W × β + ( Y × γ )

A distribuição da variável T é uma combinação da distribuição de X e de Y.

Passo 5

Como o termo que acompanha X é mais complexo, vamos analisa-lo:

W × α + 1 - W × β = Z

Z = β + α - β W

Ou seja, Z é uma combinação linear de W. Podemos descobrir qual é a média, variância e desvio padrão dessa distribuição. Pelas fórmulas sabemos que se:

J = c + d V

E J = c + d × E ( V )

Portanto

E Z = β + α - β E W

E Z = β + α - β × 0,7

E Z = 3 + 4 - 3 × 0,7 = 3,7 r e a i s / l i t r o

E sabendo que:

V a r J = d 2 V a r ( V )

Substituindo

V a r Z = α - β 2 V a r ( W )

Como W segue uma Bernoulli e a variância da Bernoulli é dada por p ( 1 - p ) , V a r W = 0,7 * 0,3 = 0,21 :

V a r Z = 4 - 3 × 0,21 = 0,21   r e a i s l i t r o 2

Passo 6

Reescrevendo T

T = Z X + γ Y

Em que Z e X são independentes (pois Z é uma função de W, que por sua vez é independente de X).

Para encontrarmos a distribuição, precisamos calcular os parâmetros.

Vamos calcular primeiro a média:

Assim

E T = E Z X + γ E Y

E T = E Z μ X + γ μ Y

E T = 3,7 × 30 + 30 × 0,5 = 126   r e a i s

Passo 7

Agora vamos calcular a variância e o desvio padrão, lembrando que W,X,Y são independentes.

V a r T = V a r Z X + γ 2 V a r ( Y )

Sabemos que

V a r Z X = E Z 2 X 2 - E Z X 2

V a r Z X = E Z 2 E X 2 - E X E Z 2

Temos que

E Z 2 = V a r Z + E Z 2 = 0,21 + 3,7 2 = 13,9 ( r e a i s l i t r o ) 2

Portanto

V a r Z X = E Z 2 μ x 2 + σ x 2 - E Z μ X 2

V a r Z X = 13,9 × 30 2 + 10 2 - 3,7 × 30 2

V a r Z X = 1579

Substituindo

V a r T = 1579 - 30 2 × 0,2 2 = 1615   r e a i s 2

Portanto

D P T ≅ 40,19   r e a i s .

Passo 8

(d) A probabilidade de que ele gaste ao todo no máximo 150 reais, ou seja, P r ⁡ ( T ≤ 150 ) .

A questão nos dá a sugestão de usar o Teorema da Probabilidade Total. Tá, mas como vamos usar isso?

A distribuição T depende de W, ou seja, depende do fato de colocarmos gasolina ou álcool. Para calcularmos a probabilidade de T ser menor ou igual a 150, devemos olhar para dois casos:

- Montante (T) ser menor ou igual a 150 quando colocamos álcool:

P ( T ≤ 150 ∩ W = 0 )

- Montante (T) ser menor ou igual a 150 quando colocamos gasolina:

P T ≤ 150 ∩ W = 1

Assim,

P T ≤ 150 =   P T ≤ 150 ∩ W = 0 + P T ≤ 150 ∩ W = 1

Passo 9

Que é exatamente o Teorema da Probabilidade Total:

P T ≤ 150 = P T ≤ 150 W = 0 . P W = 0 + P T ≤ 150 W = 1 . P ( W = 1 )

Calculando:

- P T ≤ 150 W = 0 → Note que aqui usaremos a distribuição calculada no ítem (b), que é quando escolhemos o álcool como combustível. Lembra que encontramos uma distribuição normal? Uma normal cujos parâmetros eram: 105 e 936.

Então, para calcular a probabilidade no intervalo T ≤ 150 faremos:

P T ≤ 150 W = 0 = P T - 105 936 ≤ 150 - 105 936

- P T ≤ 150 W = 1 → Note que aqui usaremos a distribuição calculada no ítem (a), que é quando escolhemos gasolina como combustível. Lá tínhamos encontrado uma distribuição normal cujos parâmetros entam: 135 e 1636.

Então, para calcular a probabilidade no intervalor T ≤ 150 faremos:

P T ≤ 150 W = 1 = P T - 135 1636 ≤ 150 - 135 1636

Substituindo na fórmula da Probabilidade Total teremos:

P T ≤ 150 = 0,929 × 0,3 + 0,645 × 0,7 = 0,730 .

Resposta

a)N(135,1636)

b) N(105,936)

c) E T = 126   r e a i s   e   D P T ≅ 40,19   r e a i s .

d) 0,730

Exercícios de Livros Relacionados

Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Uma pilha do tipo C está em condição de trabalho com probabilidade 0,7 , enquanto uma pilha do tipo D está em condição de trabalho com probabilidade 0,4. Uma piIha é selecionada aleatoriamente de um c
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número