Exercícios Resolvidos de Probabilidade Conjunta de V.A. Bidimensionais Discretas

Exercício 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 18 19

Enunciado

USP, Probabilidade, P2-2019.2, Teste 10

10) A tabela abaixo mostra a distribuição de probabilidade conjunta de duas variáveis discretas . Não foram mostrados os valores de e mas sabe-se que as duas variáveis são independentes.

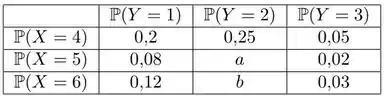
Determine .

a)

b)

c)

d)

e)

Passo 1

Faaaala pessoal, como vocês estão?

Aqui temos uma questão trabalhando o assunto de distribuição de probabilidade conjunta de variáveis aleatórias discretas. O nome é meio feio, mas vai dar certo gente, confia!

O enunciado nos mostra essa distribuição conjunta das variáveis e , mas omite dois valores, que estão na tabela como e . O objetivo do exercício é determinarmos .

Pensa comigo, os únicos pares que satisfazem são e . Daí, o que a gente quer é:

Analisando a tabela, podemos escrever que:

Puts, precisamos determinar . (que surpresa né? Haha)

E aqui é que mora o problema dessa questão: Como determinar ?

Passo 2

Uma ideia muito válida, é pensar em somar todos os pares possíveis. Pois em uma distribuição conjunta também vale que a soma de todas as probabilidades vale 1. Assim:

Mas, não facilitaram nossa vida, porque não temos apenas a incógnita , também é uma incógnita. Daí, se usarmos essa equação da soma das probabilidades ainda não vamos conseguir determinar .

Beleza então, e como é que a gente faz né? O segredo está justamente no final do enunciado, pois é falado que e são independentes.

Isso significa que:

Isso é muito bom galera, porque agora podemos montar várias equações com a nossa tabelinha do enunciado. Por exemplo:

Conseguimos “reduzir” nosso problema de determinar a determinar e .

Passo 3

Bora continuar usando essa ideia da independência de e .

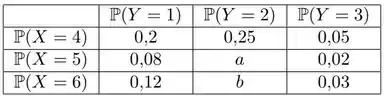
Já escrevemos no passo 2 que:

Podemos dizer também que:

Dividindo uma pela outra, vem que:

Parece que a gente trocou seis por meia dúzia, mas na verdade foi uma boa ideia porque pela tabela dá pra determinar de uma vez só. Olha, sabemos que:

Top, dividindo uma pela outra, temos:

Prontinho! Agora é só substituir na expressão de . Daí:

Isso! Conseguimos determinar . Então, agora é só correr pro abraço:

Uhuul! Conseguimos matar mais uma questão. Agora pra ver se todo mundo aprendeu bem o assunto: Qual a probabilidade de a gente ir matar mais uma questão?

(P.S: o gabarito é 1.) 😉