USP probabilidade e estatística probabilidades PSUB 2019
Duas variáveis aleatórias, , apresentam a distribuição conjunta de probabilidade dada na tabela a seguir.
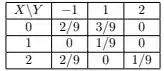
Calcule .
Passo 1
Fala pessoal, Tudo certinho com vocês? Dessa vez temos uma questão envolvendo a esperança condicional.
Bem, queremos calcular
E nos é fornecido a distribuição conjunta de . Como será que vamos começar essa questão? Vamos pensar um pouco.
Talvez seja interessante se calculássemos a distribuição de . Então vamos fazer isso.
Passo 2
Vamos começar calculando a distribuição de , Ao olharmos a tabela vemos que se então só pode assumir o valor , mas com que probabilidade isso ocorre? Isto é, quem é
Usando a definição de probabilidade condicional temos:
Onde dé a marginal de , que é dada por
Então
Ou seja,
Então a variável assume o valor com probabilidade . Logo sua esperança será:
(variável é uma contante, logo sua esperaça é essa constante)
Passo 3
Agora só nos resta verificar a distribuição de e calcular
A o olharmos a tabela, vemos que os possíveis valores de dado que são
Vamos calcular com qual probabilidade esses valores ocorrem.
Usando a definição de probabilidade condicional usada no passo anterior. Tem-se que
Onde é marginal de , que é dada por
Então
Dessa forma temos que
Então a variável assume os valores com probabilidade
Mas pera ae, não vai calcular ? Não precisamos jovem.
Pois
Passo 4
Com isso obtemos que são, respectivamente,
Finalmente acabamos a questão, pessoal!!! Espero que os passos tenham ficado claros. Até a próxima questão!! Bons estudos .