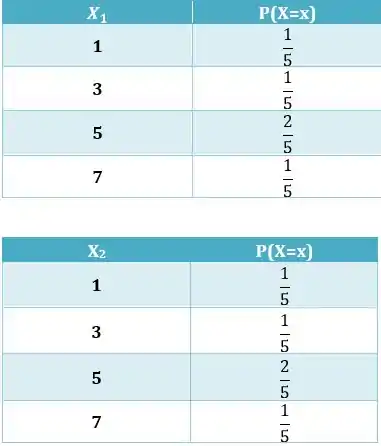
Numa urna têm-se cinco tiras de papel, numeradas 1,3,5,5,7. Uma tira é sorteada e recolocada na urna, então uma segunda tira é sorteadas. Sejam o primeiro e o segundo números sorteados.
a) Determine a distribuição
b) Obtenha as distribuições marginais de
Passo 1
a) Determine a distribuição
O primeiro passo é determinar o espaço amostral. Pelo enunciado temos um caso de retirada de urna, com reposição, portanto teremos:
Passo 2
Analisando apenas a probabilidade da primeira retirada :
Como temos 5 possibilidades (1,3,5,5,7) podemos afirmar que
Como temos duas tiras de papela do número cinco temos
Montando a tabela de distribuição marginal de .
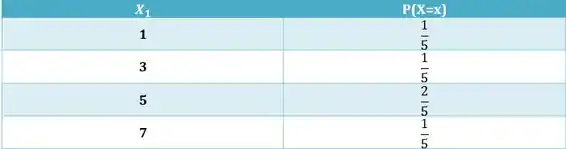
Passo 3
Analisando apenas a probabilidade da segunda retirada :
Como temos 5 possibilidades (1,3,5,5,7), pois temos a reposição, podemos afirmar que
Como temos duas tiras de papela do número cinco temos
Montando a tabela de distribuição marginal de .
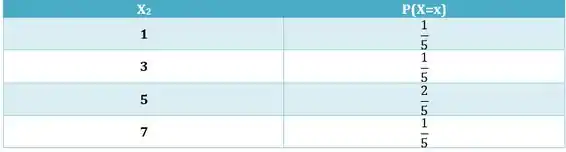
Passo 4
Montando a tabela de distribuição de .
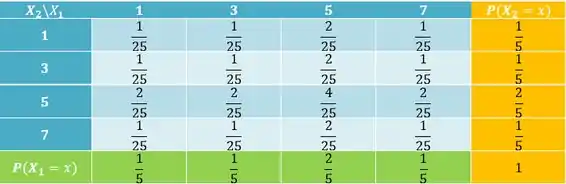
As distribuições marginais estão na última linha e na última coluna. Montamos a tabela de distribuição dos dois só para mostrar mesmo que elas SEMPRE vão aparecer e estar nas extremidades
Resposta