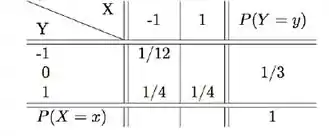
Considere a distribuição conjunta de e , parcialmente conhecida, dada pela tabela abaixo.
(a) Complete a tabela, considerando e independentes.
(b) Calcule as médias e variâncias de e .
(c) Calcule .
Passo 1
a)
Sabemos que todos os elementos da mesma linha somados tem que dar a marginal ao fim da linha, e todos os elementos da mesma coluna somados devem dar a marginal ao fim da coluna. Vamos começar por aí mesmo!
Na terceira linha, quando , podemos calcular a marginal fazendo:
Então:
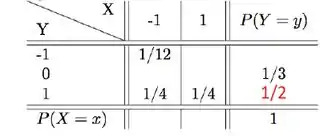
Mas nós sabemos que as marginais de mesma linha somadas tem que dar , assim como as marginais de mesma coluna. Então podemos descobrir o valor da marginal da primeira linha, para :
Então:
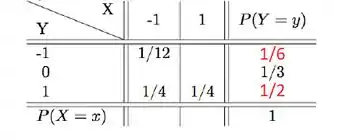
Agora podemos descobrir o valor de , pois esse é o único valor em branco da linha:
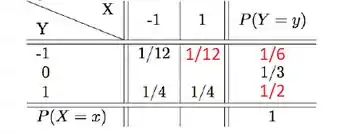
Passo 2
E agora não tem mais nada pra resolver na soma de linhas e colunas, mas como as v.a.s são independentes, podemos contornar isso aí! Sabemos que para v.a.s independentes:
Vamos fazer isso aí para a nossa primeira probabilidade conjunta:
Substituindo pelos valores que já conhecemos, podemos achar o valor desconhecido :
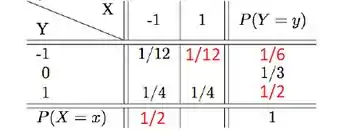
Agora podemos voltar a somar as linhas e as colunas:
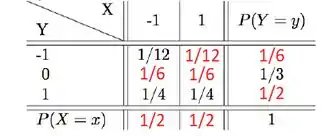
Reparem que aqui poderíamos ter achado esses valores em diferentes ordens, ou até usando a propriedade das v.a.s independentes ao invés de somar as linhas e colunas.
Passo 3
b)
Primeiro a média de , calculamos normalmente uma média unidimensional:
Agora a de :
Agora a variância de :
E a de :
Passo 4
c)
Agora vamos pensar sobre . Primeiro na . Olhando os valores que e podem assumir, vemos que a soma das duas só pode dar quando e . Então:
Agora vamos ver quando para descobrir o valor de . Reparem que o produto das variáveis só pode dar zero quando uma delas valer zero. Mas só o pode assumir valor zero! Então:
Vamos escrever nossa condicional aberta agora que sabemos os valores então:
Mas sabemos que , certo? É como se quisessmos a interseção de um conjunto dentro de outro, então a interseção tem que ser o menor desses conjuntos! Nossa condicional fica então:
Substituindo os valores que temos na tabela:
Resposta
a)
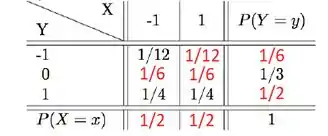
b)
c)