Considere uma onda luminosa plana, com comprimento de onda de incidindo sobre uma rede de difração com fendas separadas igualmente de entre si. Observando a imagem projetada em uma parede a um metro de distância, observa-se que existe um máximo em um ponto localizado a um metro do máximo central.
Qual a ordem deste máximo?
Passo 1
Primeiro, vamos calcular a densidade de fendas desta rede de difração ( ). Ela vai ser o inverso da distância entre as fendas:
A posição do máximo de ordem vai ser:
A ordem desse máximo vai ser:
Pelo enunciado, o comprimento de onda vale e já achamos . Porém, não temos o seno do ângulo! No caso de redes de difração, se o enunciado não falar nada, então NÃO podemos usar a aproximação de pequenos ângulos. Vamos então para o próximo passo.
Passo 2
Para achar o ângulo deste máximo, podemos achar sua tangente. O enunciado diz que a distância da rede ao anteparo é e que a distância do centro da figura até este máximo é , e por isso:
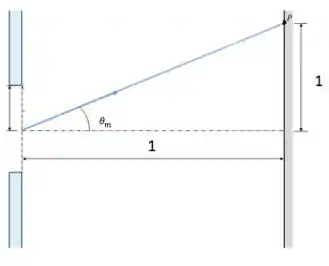
O ângulo cuja tangente é é . O seu seno vale . Substituindo na nossa equação para a ordem do ângulo:
Este é o máximo de ordem , como diz a alternativa .
Resposta
Alternativa