Uma rede de difração tem ranhuras por milímetro e é iluminada por luz branca com incidência normal. Uma figura de difração é observada em uma tela, a da rede.
Se um furo quadrado com de lado é aberto na tela com o lado interno a do máximo central e paralelo a esse máximo, determine:
- O menor comprimento de onda da luz que passa pelo furo.
- O maior comprimento de onda da luz que passa pelo furo.
Passo 1
Letra a)
Para redes de difração, as franjas brilhantes são dadas por:
Assim, a ordem do máximo que apareceria no buraco para um dado comprimento de onda é:
Digamos que apenas o máximo de uma dada ordem aparecesse. Nesse caso, quanto mais longe do centro da figura a luz batesse, maior precisaria ser o comprimento de onda para produzir uma franja no lugar.
Assim, o menor comprimento de onda que passa pelo furo vai passar pelo lado interno do furo.
Passo 2
Como o lado interno do furo está a uma distância de do centro da tela, que está a da rede de difração, o ângulo dele será:
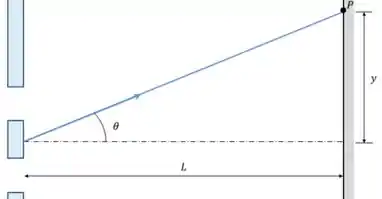
Lembrando que o enunciado nos diz que:
Substituindo:
Para a luz branca (espectro visível), considera-se em geral os comprimentos de onda de a e, nessa faixa, o único valor que nos dá um valor inteiro nessa divisão é
Passo 3
Letra b)
Iremos repetir o que fizemos para a letra a, mas dessa vez com a borda superior do furo ( quanto mais longe do máximo central, maior o comprimento de onda).
Neste caso, a altura é
E o valor máximo de comprimento de onda que passa pelo furo é .
Resposta
Letra a)
Letra b)