Uma rede de difração com 180 ranhuras por mm é iluminada na perpendicular com luz que contém os comprimentos de onda 𝜆1 = 400 𝑛𝑚 e 𝜆2 = 500 𝑛𝑚. Encontre a primeira posição angular mais próxima do centro da imagem na qual há superposição dos máximos desses diferentes comprimento de onda
Passo 1
Como sabemos que o comportamento entre todas as fendas é a mesma, vamos analisar apenas duas fendas consecutivas e descobrir o seu comportamento
Vamos entender visualmente o que o enunciado está falando
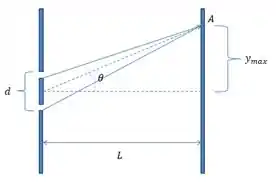
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distância entre as fendas e L a distância até o anteparo.
Mas o que o exercício quer?
O exercício quer que encontremos a primeira posição angular mais próxima do centro da imagem na qual há superposição dos máximos desses diferentes comprimento de onda
Passo 2
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Não sabemos ainda a distância entre cada fenda, mas sabemos que existem 180fendas/mm, ou seja, se dividirmos 1mm pelo número de fendas nele, encontraremos a distância entre cada fenda.
Logo
Sabemos também que
Se isolarmos as fórmulas para cada um do comprimentos de ondas teremos que
Mas sabemos que como queremos que eles se sobreponham devemos admitir que
Igualando ambos os lados das equações teremos que
Substituindo os comprimentos de ondas, teremos que
Como queremos que seja a menor distância até o centro da figura a menor escolha que podemos fazer é para = 5 𝑒 = 4.
Como já temos esses valores podemos substituir em qualquer uma das fórmulas que encontraremos o mesmo ângulo
Logo os ângulos serão