Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Redes de Difração

Ver Teoria
Exercício 19123456789101112131415161718202122232425262728

Enunciado

PUC, Física 4, P4 2016.1, 2

Uma rede de difração com 180 ranhuras por mm é iluminada perpendicularmente com luz que contém os comprimentos de onda 𝜆1 = 400 𝑛𝑚 e 𝜆2 = 500 𝑛𝑚.

(b) Encontre a separação angular entre os máximos principais de segunda ordem (m = 2) desses dois comprimentos de onda.

Passo 1

Como sabemos que o comportamento entre todas as fendas é a mesma, vamos analisar apenas duas fendas consecutivas e descobrir o seu comportamento

Vamos entender visualmente o que o enunciado está falando

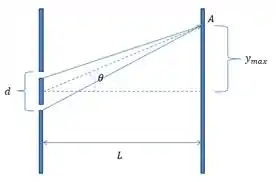
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distancia entre as fendas e L a distancia até o anteparo.

Mas o que o exercício quer?

Ele quer que determinemos a distância angular entre as franjas 1 e 2, ou seja, qual a diferença entre os ângulos dos máximos quando temos m=2.

Passo 2

Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula

d .   S e n θ = m   .   λ

Não sabemos ainda a distância entre cada fenda, mas sabemos que existem 180fendas/mm, ou seja, se dividirmos 1mm pelo número de fendas nele, encontraremos a distância entre cada fenda.

Logo

d = 1 180 = 5,56 x 10 - 3 m m = 5,56 x 10 - 6 m

Sabemos também que

λ 1   =   400   n m = 400 x 10 - 9 m    

λ 2   =   500   n m = 500 x 10 - 9 m

m = 2

Basta agora determinar o ângulo de cada um dos comprimentos de ondas para podermos achar a distância angular.

  S e n θ = m   .   λ d

S e n θ 1 = m   .   λ 1 d

S e n θ 2 = m   .   λ 2 d

Substituindo teremos que

S e n θ 1 = 2   x   400 x 10 - 9 5,56 x 10 - 6 = 0,144

S e n θ 2 = 2   x   500 x 10 - 9 5,56 x 10 - 6 = 0,179

Logo os ângulos serão

θ 1 = 8,28 °

θ 2 = 10,31 °

Logo a distância angular entre os comprimentos de ondas será dada por

∆ θ = θ 2 - θ 1 = 10,31 ° - 8,28 ° ≅ 2,1 ° ≅ 0,036 R a d

Resposta

∆ θ ≅ 2,1 ° ≅ 0,036 R a d

Exercícios de Livros Relacionados

Uma rede de difração tem n linhas por unidade de comprimento. Mostre que a separação angular ( ∆ θ ) entre duas linhas de comprimentos de onda λ e λ + ∆ λ é aproximadamente ∆ θ = ∆ λ 1 n 2 m 2 - λ 2 ,
Para uma rede de difração na qual todas as superfícies são normais à radiação incidente, a maior parte da energia está na ordem zero, a qual é inútil do ponto de vista espectroscópio, pois todos os co
Uma rede de difração com 2000 fendas por centímetro, duas linhas no espectro de primeira ordem do hidrogênio são encontradas nos ângulos de 9.72x10 - 2r a d e 1.32x10 - 1r a d . Quais são os comprimen
Uma rede de difração tem 2000 fendas por centímetro e é usada para analisar o espectro do mercúrio. (a) Determine a separação angular no espectro de primeira ordem das duas linhas com comprimentos de
Uma rede de difração com 2000 fendas por centímetro é usada para medir comprimentos de onda emitidos por gás hidrogênio. (a) Em que ângulos no espectro de primeira ordem você esperaria encontrar as du