UFF, Física 3, P3 2017.2, 14
Uma fonte de luz branca é constituída de uma mistura das seguintes cores: azul (comprimento de onda de 400 nm), verde (comprimento de onda de 500 nm), laranja (comprimento de onda de 600 nm) e vermelho (comprimento de onda de 700 nm). Um estudante observa os padrões de interferência gerados por esta luz quando ela incide sobre uma rede de difração com 100 linhas/mm em um anteparo a 2,0 metros de distância. Qual o espaçamento entre os primeiros máximos de interferência das cores verde e laranja? (Considere, para a resolução deste problema, a aproximação para pequenos ângulos)
A) 2,0 cm
B) 4,0 cm
C) 6,0 cm
D) 8,0 cm
E) 10,0 cm
Passo 1
Como sabemos que o comportamento entre todas as fendas é a mesma, vamos analisar apenas duas fendas consecutivas e descobrir o seu comportamento
Vamos entender visualmente o que o enunciado está falando
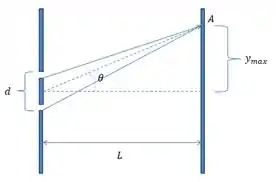
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distancia entre as fendas e L a distancia até o anteparo.
Mas o que o exercício quer?
Ele quer que determinemos a distancia entre as franjas verdes e laranjas, ou seja, de quantos em quantos metros vemos uma franja verde em seguida uma laranja, ou seja, ele quer basicamente a distancia entre dois dessas cores.
Passo 2
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Em que m= 0,
Mas lembra que os ângulos que usamos são pequenos ?
Com isso podemos usar a relação que diz
Essa relação só vale para ângulos pequenos.
Passo 3
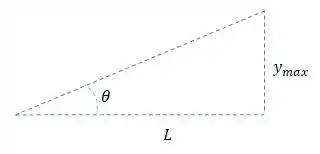Mas pelo exemplo vemos que
E sabemos que a nossa fórmula para franjas claras é
E que para ângulos pequenos vale a relação
Substituindo teremos que
Com isso concluímos que o nosso vai ser dado pela fórmula
Passo 4
Como queremos a distancia mínima entre duas franjas usaremos os valores de diferença para m=0 e m=1
Essa fórmula nos da a distância dos pontos claros de cada cor até o centro do anteparo, ou seja, se calcularmos a distancia de cada cor até o centro encontraremos a distancia entre as franjas de cada cor.
Sabemos que
Não sabemos ainda a distancia entre cada fenda, mas sabemos que existem 100fendas/mm, ou seja, se dividirmos 1mm pelo numero de fendas nele, encontraremos a distancia entre cada fenda.
Logo
Agora que já temos os valores vamos substituir para cada uma das cores
Logo a distancia entre os máximos de interferência verdes e laranjas é dado por
Resposta
a)