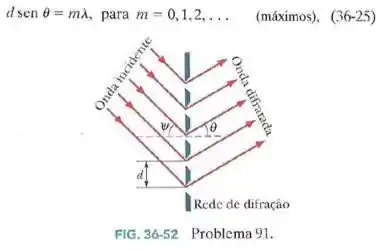
Uma luz incide em uma rede de difração fazendo um ângulo com o plano da rede, como mostra a Fig.36-52. Mostre que franjas claras ocorrem em ângulos que satisfazem a equação
, para
(Compare essa equação com a Eq.36-25). Apenas o caso especial foi tratado.
Passo 1
Precisamos apenas verificar a diferença de fase entre duas fendas, pois todas as fendas têm mesma distância até sua vizinha.
Quando a luz chega inclinada à rede de difração, os raios têm uma diferença de fase causada pela diferença de percurso.
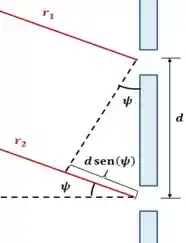
Pela imagem, vemos que a diferença de percurso é de .
A diferença de fase em múltiplos do comprimento de onda é:
Passo 2
A luz sai da rede de difração com um ângulo para atingir um ponto qualquer num anteparo longe. Para podermos visualizar a diferença de fase:
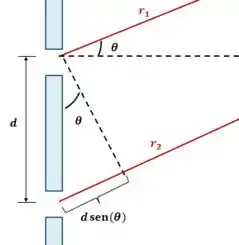
A diferença de percurso na saída vai ser:
Passo 3
A diferença de fase total vai ser a soma das duas:
Quando a diferença for um múltiplo inteiro do comprimento de onda, teremos um máximo de interferência. Ou seja:
Resposta
Ei, a resposta está no passo a passo :)