Considere que a placa seja substituída por uma rede de difração de 1,0 cm de comprimento, com fendas bastante mais estreitas, mas com o mesmo espaçamento anterior de 4,90µm. Sobre a rede, incide-se perpendicularmente luz com comprimentos de onda dentro do espectro do visível, de 400 a 700 .

(c) Qual é a região angular em que se espalham os máximos de primeira ordem? Qual cor aparece mais próxima do máximo central?

No primeiro item da pergunta deseja-se saber qual a região angular pela a qual se espalham os máximos de primeira ordem, o que devemos perceber primeiro é que, como ele fala sobre máximo de primeira ordem, temos que

O que significa que a nossa fórmula pode ser escrita como

Agora como faremos para descobrirmos a região angular?

Basta que avaliemos os dois extremos do espectro visível, que no caso, no enunciado foi dado que vai de até , com isso teremos que

Sabendo que

E

E que ainda

Substituindo os valores teremos que

E

Agora que já determinamos a região angular, falta apenas determinarmos a cor que irá aparecer mais próxima ao centro, para isso temos uma solução bem simples, pense da seguinte maneira, a nossa distribuição angular se da como a figura abaixo

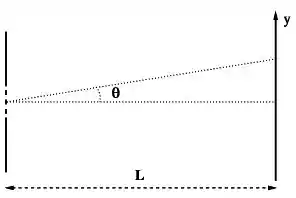
Podemos ver que o ângulo vai aumentando conforme a distância vertical vai aumentando, como queremos a cor próxima ao centro, significa que queremos valores de ângulo menores, quando no caso o valor de é pequeno. Vamos olhar a nossa fórmula

Sabemos que m=1, logo

Se temos valores pequenos de temos os menores comprimentos de ondas relacionados aos menores ângulos. Como vimos no passo anterior, o menor ângulo ocorreu para o menor comprimento de onda, que nesse caso é de 400nm. Se olharmos o espectro visível

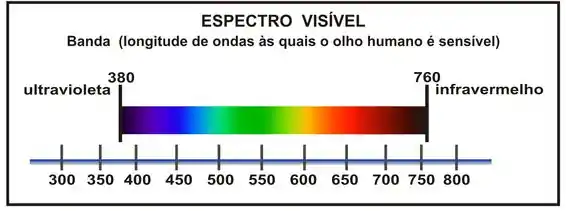
Vemos que o comprimento de onda de ocorre na cor violeta, logo, será essa a cor próxima ao centro.