Considere uma rede de difração com ranhuras por milímetro. A rede é iluminada com um feixe estreito de luz verde , que incide perpendicularmente sobre a mesma.
Os feixes têm intensidade e diâmetro igual a . O padrão de interferência é formado sobre um anteparo paralelo à rede de difração situado a de distância.
- Calcule o número de ranhuras que atuarão efetivamente como fontes secundárias (ou fontes de Huygens) nesta experiência.
- Calcule o valor máximo da razão .
- Calcule a diferença angular entre os dois mínimos adjacentes ao máximo central.
- Quantos zeros há entre o máximo central e um máximo de primeira ordem?
- Escolha uma escala apropriada e faça um esboço do gráfico da razão em função de representando o máximo central e a disposição do primeiro zero.
Passo 1
Letra (a): Calcule o número de ranhuras que atuarão efetivamente como fontes secundárias (ou fontes de Huygens) nesta experiência.
Como a rede de difração possui 400 ranhuras por milímetro e é iluminada por um feixe de diâmetro igual a , somente as ranhuras iluminadas atuarão como fontes secundárias, logo.
Passo 2
Letra (b): Calcule o valor máximo da razão .
O maior valor da razão se dará no maior valor possível de , isso acontece justamente no máximo central.
Quando falamos de intensidade, vimos que o valor dos máximos principais são proporcionais a , assim, no máximo central:
Logo:
Passo 3
Letra (c): Calcule a diferença angular entre os dois mínimos adjacentes ao máximo central.
Os ângulos em que encontramos mínimos de interferência são dados por:
Assim, a diferença angular entre os dois mínimos adjacentes ao máximo central será:
Onde , logo:
Passo 4
Letra (d): Quantos zeros há entre o máximo central e um máximo de primeira ordem?
Conforme vimos em Interferência e em Difração para fendas, entre cada dois máximos principais existem zeros.
Logo:
Passo 5
Letra (e): Escolha uma escala apropriada e faça um esboço do gráfico da razão em função de representando o máximo central e a disposição do primeiro zero.
Algumas informações que já temos de antemão é que, para fendas, a altura do máximo central é proporcional a , e que a largura do máximo central é proporcional a .
Assim, um gráfico apropriado de é algo do tipo:
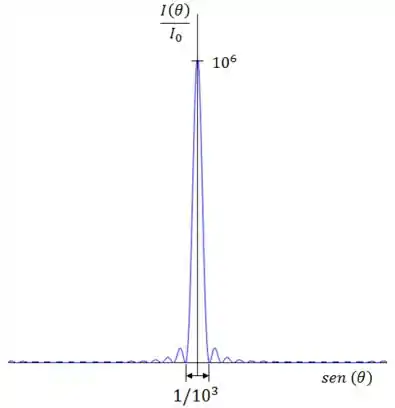
Lembrando que, nesse tipo de questão, não é necessário que você faça algo exatamente igual, mas é importante colocar algumas informações que você já possui. ;)
Resposta
Letra (a):
Letra (b):
Letra (c):
Letra (d):
Letra (e):